题目内容
15.方程xy2-x2y=8x所表示的曲线( )| A. | 关于y轴对称 | B. | 关于y+x=0对称 | C. | 关于原点对称 | D. | 关于x-y=0对称 |
分析 设(a,b)点在曲线上,则(a,b)点满足方程xy2-x2y=8x,进而我们可以判断出(-a,-b)也满足方程xy2-x2y=8x,即(-a,-b)也在曲线上,进而可以得到结论.
解答 解:若(a,b)点在曲线上,则ab2-a2b=8a
令x=-a,y=-b,则(-a)(-b)2-(-a)2(-b)=-(ab2-a2b)=8(-a)
即(-a,-b)点也在曲线上
故方程xy2-x2y=8x所表示的曲线关于原点对称
故选:C.
点评 本题考查的知识点是曲线的对称性,当(a,b)点在曲线上时,(-a,-b)点也在曲线上,则曲线关于原点对称;当(a,b)点在曲线上时,(-a,b)点也在曲线上,则曲线关于y轴对称;当(a,b)点在曲线上时,(a,-b)点也在曲线上,则曲线关于x轴对称;当(a,b)点在曲线上时,(b,a)点也在曲线上,则曲线关于直线x-y=0对称;当(a,b)点在曲线上时,(-b,-a)点也在曲线上,则曲线关于直线x+y=0对称.

练习册系列答案
相关题目
6.已知实数x、y满足$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$,则z=2x-y的取值范围是( )
| A. | [-5,7] | B. | [5,7] | C. | [4,7] | D. | [-5,4] |
10.$\int_0^1{[\sqrt{1-{{(x-1)}^2}}}-x]dx$的值为( )
| A. | $\frac{π}{2}-1$ | B. | 2 | C. | $\frac{π}{4}-\frac{1}{2}$ | D. | 4 |
20.已知某三棱锥的三视图如图所示,则它的外接球体积为( )
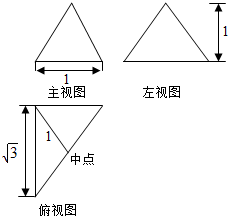

| A. | $\frac{32}{3}π$ | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{{\sqrt{2}}}{3}π$ |
7.过抛物线y2=4x的焦点F作倾斜角为60°的直线,交抛物线于A,B两点(A在x轴上方),那么$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 3 | D. | 2 |
4.A、B两人约定在星期天上午在紫阳公园会面,并约定先到者须等候一刻钟,过时即可离去;若A是6点半到达,假设B在6点到7点之间的任何时刻到达是等可能的,则两人能会面的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |