题目内容
【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B= ![]()
(1)求边c的长;
(2)求角B的大小.
【答案】
(1)解:∵acosB=3,bcosA=l,∴a× ![]() =3,b×
=3,b× ![]() =1,
=1,
化为:a2+c2﹣b2=6c,b2+c2﹣a2=2c.
相加可得:2c2=8c,解得c=4
(2)解:由(1)可得:a2﹣b2=8.
由正弦定理可得: ![]() =
= ![]() =
= ![]() ,
,
又A﹣B= ![]() ,∴A=B+
,∴A=B+ ![]() ,C=π﹣(A+B)=
,C=π﹣(A+B)= ![]() ,可得sinC=sin
,可得sinC=sin ![]() .
.
∴a= 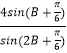 ,b=
,b= ![]() .
.
∴ ![]() ﹣16sin2B=
﹣16sin2B= ![]() ,
,
∴1﹣ ![]() ﹣(1﹣cos2B)=
﹣(1﹣cos2B)= ![]() ,即cos2B﹣
,即cos2B﹣ ![]() =
= ![]() ,
,
∴﹣2 ![]() ═
═ ![]() ,
,
∴ ![]() =0或
=0或 ![]() =1,B∈
=1,B∈ ![]() .
.
解得:B= ![]()
【解析】(1)由acosB=3,bcosA=l,利用余弦定理化为:a2+c2﹣b2=6c,b2+c2﹣a2=2c.相加即可得出c.(2)由(1)可得:a2﹣b2=8.由正弦定理可得: ![]() =
= ![]() =
= ![]() ,又A﹣B=
,又A﹣B= ![]() ,可得A=B+
,可得A=B+ ![]() ,C=
,C= ![]() ,可得sinC=sin
,可得sinC=sin ![]() .代入可得
.代入可得 ![]() ﹣16sin2B=
﹣16sin2B= ![]() ,化简即可得出.
,化简即可得出.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目