题目内容
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取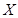 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或
抽取的人数达到4位,则停止抽取,求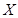 的分布列及数学期望.
的分布列及数学期望.
(Ⅰ)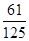 (Ⅱ)
(Ⅱ)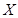
2 3 4 
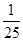
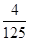
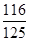
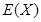
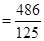
解析试题分析:(Ⅰ)依题意可得,任意抽取一位市民会购买本地家禽的概率为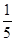 ,
,
从而任意抽取一位市民不会购买本地家禽的概率为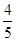 .
.
设“至少有一位市民会购买本地家禽”为事件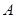 ,则
,则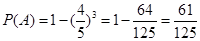 ,
,
故至少有一位市民会购买本地家禽的概率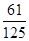 . 4分
. 4分
(Ⅱ)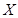 的所有可能取值为:2,3,4.
的所有可能取值为:2,3,4.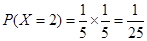 ,
,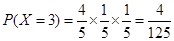 ,
,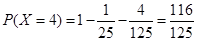 ,
,
所以 的分布列为:
的分布列为:
10分
2 3 4 
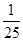
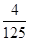
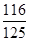
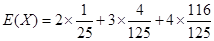
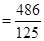 . 12分
. 12分
考点:概率分布列
点评:第一问考察的是独立重复试验概率问题:每次试验事件A发生的概率为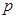 ,
,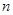 次重复试验有
次重复试验有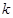 次发生的概率为
次发生的概率为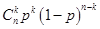 ;求分布列的步骤:找到随机变量可以取得值,求出各随机变量对应的概率,汇总成分布列
;求分布列的步骤:找到随机变量可以取得值,求出各随机变量对应的概率,汇总成分布列

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
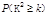 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
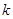 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
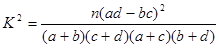 (
(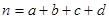 )
) 某大学高等数学老师这学期分别用 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| | 甲班 | 乙班 | 合计 |
| 优秀 | | | |
| 不优秀 | | | |
| 合计 | | | |
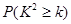 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
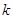 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中
其中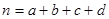 )
) 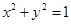 相切的概率;
相切的概率;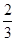 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.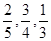 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.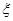 ,试求
,试求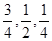 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.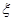 ,求
,求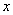 ,
,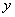 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.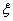 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时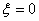 ,求
,求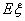 .
.