题目内容
设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2) 若 是从区间[0,3] 任 取 的一个数,
是从区间[0,3] 任 取 的一个数,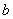 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
(1)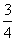 (2)
(2)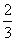
解析试题分析:记事件A为“方程x2+2ax+b2=0有实根”,
当a≥0,b≥0时,方程x2+2ax+b2=0有实根的充要条件为a≥b.
(1)基本事件共有12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示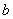 的取值.
的取值.
事件A中包含9个基本事件,事件A发生的概率为P(A)=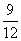 =
=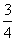 .
.
(2)试验的全部结果所构成的区域为{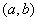 |0≤a≤3,0≤b≤2}.
|0≤a≤3,0≤b≤2}.
构成事件A的区域为{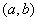 |0≤a≤3,0≤b≤2,a≥b},所以所求的概率为
|0≤a≤3,0≤b≤2,a≥b},所以所求的概率为
P(A)=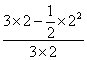 =
=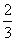 .
.
考点:等可能事件的概率
点评:本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现,有时文科会考这种类型的解答题.

练习册系列答案
相关题目
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立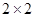 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
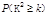 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
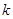 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
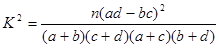 (
(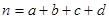 )
) 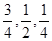 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.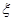 ,求
,求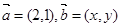
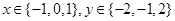 ,求向量
,求向量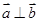 的概率;
的概率;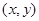 构成区域
构成区域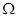 :
: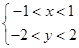 ,求二元数组
,求二元数组
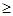 1的概率.
1的概率.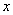 ,
,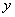 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.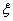 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时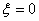 ,求
,求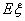 .
.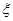 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求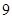 的
的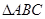 内任投一点
内任投一点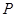 ,求
,求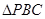 的面积小于
的面积小于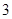 的概率?
的概率?