题目内容
已知函数 ,
, ,(
,(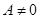 )
)
(1)当
 ≤
≤ ≤
≤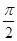 时,求
时,求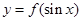 的最大值;
的最大值;
(2)若对任意的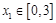 ,总存在
,总存在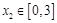 ,使
,使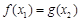 成立,求实数
成立,求实数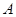 的取值范围;
的取值范围;
(3)问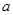 取何值时,方程
取何值时,方程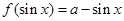 在
在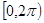 上有两解?
上有两解?
【答案】
(1)当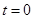 时,
时,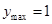 ;(2)
;(2)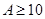 或
或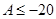 ;(3)
;(3)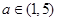 或
或 。
。
【解析】
试题分析:(1)
设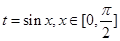 ,则
,则
∴
∴当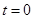 时,
时,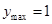
(2)当 ∴
∴ 值域为
值域为
当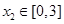 时,则
时,则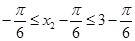
有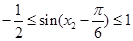
①当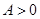 时,
时,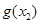 值域为
值域为
②当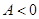 时,
时,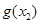 值域为
值域为
而依据题意有 的值域是
的值域是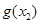 值域的子集
值域的子集
则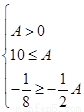 或
或 
∴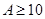 或
或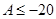
(3) 化为
化为
 在
在 上有两解,
上有两解,
令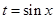 则t∈
则t∈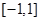
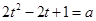 在
在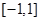 上解的情况如下:
上解的情况如下:
①当在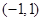 上只有一个解或相等解,
上只有一个解或相等解,
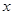 有两解
有两解 或
或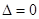
∴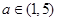 或
或
②当 时,
时,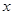 有惟一解
有惟一解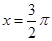
③当 时,
时,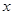 有惟一解
有惟一解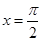
故 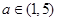 或
或
考点:本题主要考查三角函数的和差倍半公式,三角函数、二次函数的图象和性质。
点评:中档题,本题综合考查三角函数的和差倍半公式,三角函数、二次函数的图象和性质。应用三角公式对三角函数式进行化简,以便于利用其它知识解题,是这类题的显著特点。本题利用“换元法”,将问题转化成二次函数问题。在解方程的过程中,要特别注意解答范围。

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|