题目内容
5.在交通拥挤及事故多发地段,为了确保交通安全,规定在此地段内,车距d是车速v(公里/小时)的平方与车身长S(米)的积的正比例函数,且最小车距不得小于车身长的一半,现假定车速为50公里/小时,车距恰好等于车身长,试写出d关于v的函数关系式(其中S为常数).分析 根据车距d是车速v(千米/小时)的平方与车身长s(米)之积的正比例函数,可假设函数解析式.利用车速为50千米/小时,车距恰为车身长.可求d关于v的解析式.
解答 解:由已知:d=ksv2,车速为50公里/小时,车距恰好等于车身长,可得k=$\frac{1}{2500}$,
∴d=$\frac{1}{2500}$sv2,
当d≥$\frac{s}{2}$时,$\frac{1}{2500}$sv2≥$\frac{s}{2}$,v≥25$\sqrt{2}$
∴d=$\left\{\begin{array}{l}{\frac{s}{2},0<v<25\sqrt{2}}\\{\frac{1}{2500}s{v}^{2},v≥25\sqrt{2}}\end{array}\right.$.
点评 本题的考点是根据实际问题选择函数类型.主要考查利用待定系数法求函数解析式,关键是将实际问题转化为数学问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知某几何体的三视图如图所示,则该几何体的体积为( )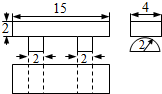

| A. | 120+16π | B. | 120+8π | C. | 120+4π | D. | 60+8π |