题目内容
设直线 的方程为
的方程为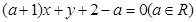 .
.
(1)若 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求 的方程;
的方程;
(2)若 不经过第二象限,求实数
不经过第二象限,求实数 的取值范围。
的取值范围。
(1)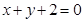 ;(2)
;(2)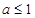 .
.
解析试题分析:(1)按直线是否经过原点两种情况讨论,分别求出 的值,从而确定直线的方程;
的值,从而确定直线的方程;
(2)因为直线的斜率一定存在,所以,由直线不过第二象限,可知直线的斜非负,在 轴上的截距非正,从面确定实数的取值范围.
轴上的截距非正,从面确定实数的取值范围.
试题解析:解(1)当直线过原点时,该直线在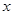 轴和
轴和 轴上的截距都为零,当然相等,
轴上的截距都为零,当然相等,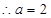 ,方程即为
,方程即为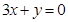 ;若
;若 ,由截距存在,
,由截距存在,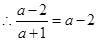 即
即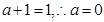 ,方程即为
,方程即为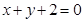 .
.
(2)将 的方程化为
的方程化为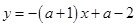 ,
,
所以,要使 不经过第二象限,当且仅当
不经过第二象限,当且仅当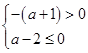 或
或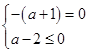
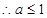
综上可知 的取值范围是
的取值范围是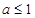 .
.
考点:直线的一般式方程与截距式的互化.

练习册系列答案
相关题目
 ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 与
与 、
、 两点,
两点, 为坐标原点.
为坐标原点. 为直径的圆的方程;
为直径的圆的方程; ,求直线
,求直线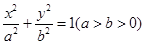 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率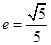 , 直线
, 直线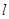 交椭圆于M,N两点.
交椭圆于M,N两点.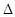 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线 ,点
,点 依次满足
依次满足 。
。 的轨迹;
的轨迹;  作直线
作直线 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到 轴的距离为
轴的距离为 ,且直线
,且直线 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出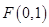 直线
直线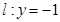 ,
,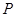 为平面上的动点,过点
为平面上的动点,过点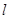 的垂线,垂足为
的垂线,垂足为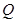 ,且
,且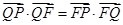 .
.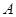 、
、 是轨迹
是轨迹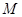 上异于坐标原点
上异于坐标原点 的不同两点,轨迹
的不同两点,轨迹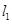 、
、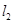 ,且
,且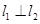 ,
, ,求点
,求点 的直线经过点
的直线经过点 ,直线的一般式方程是 ▲
,直线的一般式方程是 ▲