题目内容
已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0 .
(1)求直线l的方程; (2)求直线l关于原点O对称的直线方程。
(1)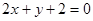 (2)
(2)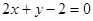
解析试题分析:(1)所求直线过另外两条直线的交点,所以先求该点,又因为所求直线与已知直线垂直,所以根据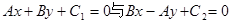 垂直,可设出所求直线,将点代入,求之.
垂直,可设出所求直线,将点代入,求之.
(2)直线关于原点对称,则直线上的点关于原点对称,找到两个特殊点,即两轴的交点,利用对称找到对称点,可求对称直线.
试题解析: (1)由题知 所以交点为
所以交点为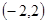
由于所求直线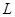 与
与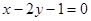 垂直,
垂直,
可设直线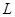 的方程为
的方程为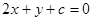 ,
,
把点的坐标代入得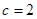 .
.
所求直线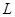 的方程为
的方程为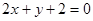 .
.
(2)因为直线关于原点对称,所以直线上的点也关于原点对称:
又因为直线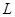 与
与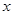 轴、
轴、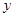 轴的交点是
轴的交点是
则直线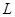 关于原点对称的直线与
关于原点对称的直线与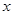 轴、
轴、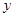 轴的交点为
轴的交点为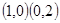
利用截距式可得,所求直线方程为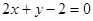
考点:两直线垂直的关系;直线关于点的对称;

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 中,对于直线
中,对于直线 :
: 和点
和点 记
记 若
若 <0,则称点
<0,则称点 被直线
被直线 被直线
被直线 被直线
被直线 分隔;
分隔; 是曲线
是曲线 的分隔线,求实数
的分隔线,求实数 的取值范围;
的取值范围; 的距离与到
的距离与到 轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.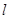 的方程为
的方程为 ,圆
,圆 的方程为
的方程为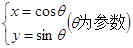 .
. 的方程为
的方程为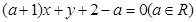 .
. 的取值范围。
的取值范围。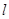 经过直线2x+y-2=0与x-2y+1=0的交点,且与直线
经过直线2x+y-2=0与x-2y+1=0的交点,且与直线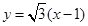 的夹角为
的夹角为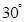 ,求直线
,求直线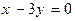 且与曲线
且与曲线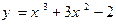 相切的直线方程的一般式_____________。
相切的直线方程的一般式_____________。