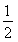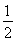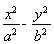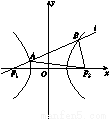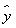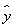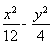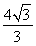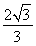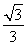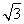题目内容
设f(x)＝ln(x2＋1)，g(x)＝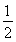
x2－
.
(1)求F(x)＝f(x)－g(x)的单调区间，并证明对[－1，1]上的任意x1，x2，x3，都有F(x1)＋F(x2)>F(x3)；
(2)将y＝f(x)的图像向下平移a(a>0)个单位，同时将y＝g(x)的图像向上平移b(b>0)个单位，使它们恰有四个交点，求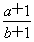
的取值范围．
（1）在(－∞，－1)和(0，1)上单调递增，在(－1，0)和(1，＋∞)上单调递减，证明见解析（2）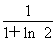
<
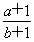<1＋ln 2
【解析】(1)F(x)＝ln(x2＋1)－
x2－
，
F′(x)＝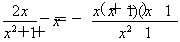
.
F′(x)，F(x)的值随x值的变化如下表：
x | (－∞，－1) | (－1，0) | (0，1) | (1，＋∞) |
F′(x) | ＋ | － | ＋ | － |
F(x) | ↗ | ↘ | ↗ | ↘ |
故F(x)在(－∞，－1)和(0，1)上单调递增，在(－1，0)和(1，＋∞)上单调递减，在[－1，1]上F(x)的最小值F(x)min＝F(0)＝.
F(x)的最大值F(x)max＝F(1)＝F(－1)＝ln 2.
因此F(x1)＋F(x2)≥2F(x)min＝1，
而F(x3)≤F(x)max＝ln 2，
故F(x1)＋F(x2)>F(x3)．
(2)由题意可知y＝ln(x2＋1)－a与y＝x2－＋b的图像恰有四个交点．
由ln(x2＋1)－a＝x2－＋b，
则a＋b＝ln(x2＋1)－x2＋.
令F(x)＝ln(x2＋1)－x2＋，
由(1)可知F(x)极小值＝F(0)＝，F(x)极大值＝F(1)＝ln 2.又F(4)＝F(－4)<0<F(0)，所以F(x)的大致图像如图所示，
图(1)
要使y＝a＋b与y＝F(x)恰有四个交点，则<a＋b<ln 2.
由
得到(b，a)的可行域为如图(2)所示的阴影部分．
图(2)
又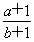可视为点P(－1，－1)与可行域内的点连线的斜率，
故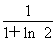<<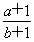1＋ln 2.
