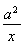题目内容
“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的( )
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
C
【解析】由题意，得f(x)＝|(ax－1)x|＝|ax2－x|.若a＝0，则f(x)＝|x|，此时f(x)在区间(0，＋∞)上单调递增．若a<0，则二次函数y＝ax2－x的对称轴x＝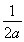
<0，且x＝0时y＝0，此时y＝ax2－x在区间(0，＋∞)上单调递减且y<0恒成立，故f(x)＝|ax2－x|在区间(0，＋∞)上单调递增．综上所述，当a≤0时，f(x)在区间(0，＋∞)上单调递增，条件是充分的．反之若a>0，则二次函数y＝ax2－x的对称轴x＝
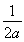>0，且在区间(0，
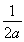)上y<0，此时f(x)＝|ax2－x|在区间(0，
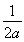)上单调递增，在区间[
，
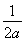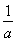]上单调递减．故函数f(x)不可能在区间(0，＋∞)上单调递增，条件是必要的．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
