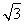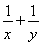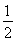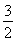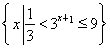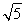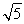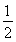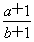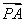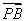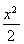设f(x)是定义在R上的偶函数.且当x≥0时.f(x)＝2x.若对任意的x∈[a.a+2].不等式f(x+a)≥f2(x)恒成立.则实数a的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

设f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝2x.若对任意的x∈[a，a＋2]，不等式f(x＋a)≥f2(x)恒成立，则实数a的取值范围是________．

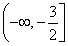
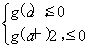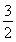【解析】根据题意知函数f(x)＝2|x|，若f(x＋a)≥f2(x)，则2|x＋a|≥(2|x|)2＝22|x|，所以|x＋a|≥2|x|，即3x2－2ax－a2≤0对任意的x∈[a，a＋2]恒成立．令g(x)＝3x2－2ax－a2，则解得a≤－，即a∈.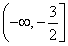

练习册系列答案

作业本江西教育出版社系列答案

相关题目

设x，y∈R，a>1，b>1，若ax＝by＝3，a＋b＝2，则的最大值为(　　)

A. B．1 C. D．2

观察下列算式：

13＝1，

23＝3＋5，

33＝7＋9＋11，

43＝13＋15＋17＋19，

……

若某数n3按上述规律展开后，发现等式右边含有“2013”这个数，则n＝________．

设集合A＝{x|－3<x<1}，B＝{x|log2|x|<1}，则A∩B等于(　　)

A．(－3，0)∪(0，1) B．(－1，0)∪(0，1) C．(－2，1) D．(－2，0)∪(0，1)

若集合A＝，B＝{x|log2x≤1}，则A∪B等于(　　)

A．(－∞，2] B．(－∞，2) C．(－2，2] D．(－2，2)

若函数f(x)＝x3－3x在(a，6－a2)上有最小值，则实数a的取值范围是(　　)

A．(－，1) B．[－，1)

C．[－2，1) D．(－2，1)

设f(x)＝ln(x2＋1)，g(x)＝x2－.

(1)求F(x)＝f(x)－g(x)的单调区间，并证明对[－1，1]上的任意x1，x2，x3，都有F(x1)＋F(x2)>F(x3)；

(2)将y＝f(x)的图像向下平移a(a>0)个单位，同时将y＝g(x)的图像向上平移b(b>0)个单位，使它们恰有四个交点，求的取值范围．

某班主任对全班30名男生进行了作业量多少的调查，数据如下表：

该班主任据此推断认为男生喜欢玩电脑游戏与作业量的多少有关，这种推断犯错误的概率不超过________．

附：K2＝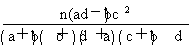

P(K2>k)	0.050	0.010	0.001
k	3.841	6.625	10.828

已知两定点A(1，1)，B(－1，－1)，动点P(x，y)满足·＝，则点P的轨迹是(　　)

A．圆 B．椭圆 C．双曲线 D．拋物线

试题分类