题目内容
7.设F为椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,点$p(1,\frac{3}{2})$在椭圆E上,直线l0:3x-4y-10=0与以原点为圆心?以椭圆E的长半轴长为半径的圆相切.(1)求椭圆E的方程;
(2)过点F的直线l与椭圆相交于A,B两点,过点P且平行于AB的直线与椭圆交于另一点Q.问是否存在直线l,使得四边形PABQ的对角线互相平分?若存在,求出l的方程;若不存在,说明理由.
分析 (1)利用点$p(1,\frac{3}{2})$在椭圆E上,直线l0:3x-4y-10=0与以原点为圆心?以椭圆E的长半轴长为半径的圆相切,建立方程求出a,b,即可求椭圆E的方程;
(2)设直线l的方程为y=k(x-1),直线PQ的方程为$y=k(x-1)+\frac{3}{2}$,分别与椭圆方程联立,求出|AB|,|PQ|.若四边形PABQ的对角线互相平分,则四边形PABQ为平行四边形,可得|AB|=|PQ|,即可得出结论.
解答 解:(1)由题意知$\left\{{\begin{array}{l}{a=\frac{{|{-10}|}}{{\sqrt{{3^2}+{4^2}}}}=2}\\{\frac{1}{a^2}+\frac{{\frac{9}{4}}}{b^2}=1}\end{array}⇒\left\{{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\end{array}}\right.}\right.$
所以椭圆E 的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$…(4分)
(2)结论:存在直线l,使得四边形PABQ的对角线互相平分.…(5分)
理由如下:由题可知直线l、PQ的斜率存在.
设直线l的方程为y=k(x-1),直线PQ的方程为$y=k(x-1)+\frac{3}{2}$
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=k(x-1)}\end{array}}\right.$消去y得(3+4k2)x2-8k2x+(4k2-12)=0
则$|{AB}|=\sqrt{1+{k^2}}\frac{{\sqrt{△_1}}}{{3+4{k^2}}}=\sqrt{1+{k^2}}\frac{{\sqrt{144({1+{k^2}})}}}{{3+4{k^2}}}$,…(7分)
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=k(x-1)+\frac{3}{2}}\end{array}}\right.$消去y得(3+4k2)x2-(8k2-12k)x+(4k2-12k-3)=0
则$|{PQ}|=\sqrt{1+{k^2}}\frac{{\sqrt{△_2}}}{{3+4{k^2}}}=\sqrt{1+{k^2}}\frac{{\sqrt{144({\frac{1}{4}+k+{k^2}})}}}{{3+4{k^2}}}$,…(9分)
若四边形PABQ的对角线互相平分,则四边形PABQ为平行四边形,
∴|AB|=|PQ|,
∴$1+{k^2}=\frac{1}{4}+k+{k^2}⇒k=\frac{3}{4}$
∴直线l的方程为3x-4y-3=0时,四边形PABQ的对角线互相平分.…(12分)
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,有难度.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
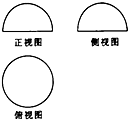
| A. | 半球 | B. | 球 | C. | 圆柱 | D. | 圆锥 |
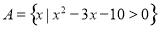 ,集合
,集合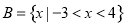 ,则
,则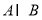 等于( )
等于( )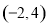 B.
B.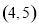
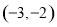 D.
D.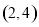
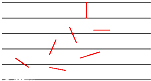 十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.