题目内容
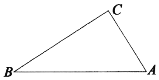
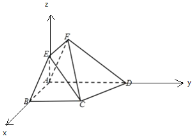
【题目】如图,四边形ABCD为直角梯形,BC∥AD,∠BAD=90°,BC=2,AD=3,四边形ABEF为平行四边形,AB=1,BE=2,∠EBA=60°,平面ABEF⊥平面ABCD.
(1)求证:AE⊥平面ABCD;
(2)求平面ABEF与平面FCD所成锐二面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)在平行四边形![]() 中求得
中求得![]() 的长,用勾股定理逆定理证明
的长,用勾股定理逆定理证明![]() ,然后由面面垂直的性质定理得线面垂直;
,然后由面面垂直的性质定理得线面垂直;
(2)以A为原点,AB为x轴,AD为y轴,AE为z轴,建立空间直角坐标系,写出各点坐标,求出平面法向量,由法向量夹角得二面角.
(1)证明:∵四边形ABEF为平行四边形,AB=1,BE=2,∠EBA=60°,
∴AE![]() ,
,
∴AB2+AE2=BE2,∴AB⊥AE,
∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB.
∴AE⊥平面ABCD.
(2)解:∵四边形ABCD为直角梯形,BC∥AD,∠BAD=90°,BC=2,AD=3,
∴以A为原点,AB为x轴,AD为y轴,AE为z轴,建立空间直角坐标系,
则A(0,0,0),B(1,0,0),E(0,0,![]() ),F(﹣1,0,
),F(﹣1,0,![]() ),C(1,2,0),D(0,3,0),
),C(1,2,0),D(0,3,0),
![]() (1,0,0),
(1,0,0),![]() (2,2,
(2,2,![]() ),
),
设平面FCD的法向量![]() (x,y,z),
(x,y,z),
则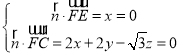 ,取y
,取y![]() ,得
,得![]() (0,
(0,![]() ,2),
,2),
平面ABEF的法向量![]() (0,1,0),
(0,1,0),
设平面ABEF与平面FCD所成锐二面角的平面角为θ,
则cosθ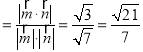 .
.
∴平面ABEF与平面FCD所成锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目