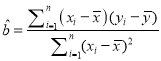题目内容
【题目】公元![]() 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
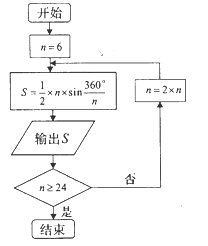
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中![]() 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
(参考数据: ![]() )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
【答案】B
【解析】解:结合题中所给的流程图可知,输出的![]() 值为:
值为:
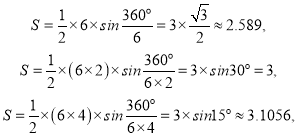
综上可得:执行此算法输出的圆周率的近似值依次为2.598,3,3.1056.
本题选择B选项.

练习册系列答案
相关题目
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.