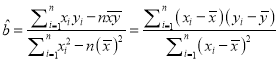Question

【题目】在数列{an}，{bn}中，a1＝2，b1＝4，且an，bn，an＋1成等差数列，bn，an＋1，bn＋1成等比数列{n∈N＋}．

求a2，a3，a4及b2，b3，b4，由此猜测{an}，{bn}的通项公式，并证明你的结论；

Answer 1

【答案】a2＝6，b2＝9，a3＝12，b3＝16，a4＝20，b4＝25.证明见解析.

猜测an＝n(n＋1)，bn＝(n＋1)2，n∈N*.

【解析】主要考查了数列的通项公式和数学归纳法的运用。

由条件得2bn＝an＋an＋1， ＝bnbn＋1，

由此可得a2＝6，b2＝9，a3＝12，b3＝16，a4＝20，b4＝25.

猜测an＝n(n＋1)，bn＝(n＋1)2，n∈N*.

用数学归纳法证明：

①当n＝1时，由已知a1＝2，b1＝4可得结论成立．

②假设当n＝k(k≥2且k∈N*)时，结论成立，即

ak＝k(k＋1)，bk＝(k＋1)2，

那么当n＝k＋1时，

ak＋1＝2bk－ak＝2(k＋1)2－k(k＋1)＝(k＋1)(k＋2)，

bk＋1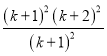＝＝＝(k＋2)2.

解：由条件得2bn＝an＋an＋1， ＝bnbn＋1，

由此可得a2＝6，b2＝9，a3＝12，b3＝16，a4＝20，b4＝25.

猜测an＝n(n＋1)，bn＝(n＋1)2，n∈N*. 4分

用数学归纳法证明：

①当n＝1时，由已知a1＝2，b1＝4可得结论成立．

②假设当n＝k(k≥2且k∈N*)时，结论成立，即

ak＝k(k＋1)，bk＝(k＋1)2，

那么当n＝k＋1时，

ak＋1＝2bk－ak＝2(k＋1)2－k(k＋1)＝(k＋1)(k＋2)，

bk＋1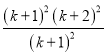＝＝＝(k＋2)2.

所以当n＝k＋1时，结论也成立．

由①②可知，an＝n(n＋1)，bn＝(n＋1)2对一切n∈N*都成立． 10分