题目内容
【题目】已知数列![]() 前
前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,
,![]() 为
为![]() 的前
的前![]() 项和,求证:
项和,求证:![]() .
.
(3)在(2)的条件下,若数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,求证
,求证![]()
(4)请你说明第(3)问所用到的求和方法,哪些数列通项的模型适合此方法?请举例说明.(至少列举出三种)
【答案】(1)![]() (2)证明见解析(3)证明见解析(4)裂项相消法,说明见解析(答案不唯一)
(2)证明见解析(3)证明见解析(4)裂项相消法,说明见解析(答案不唯一)
【解析】
(1)当![]() 时
时![]() ,与条件作差可得
,与条件作差可得![]() ,讨论是否满足
,讨论是否满足![]() ,进而求解即可;
,进而求解即可;
(2)由(1),![]() ,则
,则![]() ,进行放缩可得
,进行放缩可得![]() ,进而利用裂项相消法求解即可;
,进而利用裂项相消法求解即可;
(3)由(2),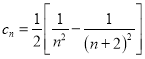 ,进而利用裂项相消法求解即可;
,进而利用裂项相消法求解即可;
(4)第(3)问使用的是裂项相消的求和方法,举例说明即可.
(1)因为![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() ,则
,则![]() ,满足上式,
,满足上式,
所以数列![]() 是首项为2,公比为4的等比数列,
是首项为2,公比为4的等比数列,
所以![]()
(2)证明:由(1),则![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
则![]()
(3)证明:由(2),则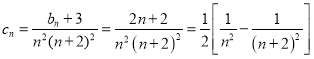 ,
,
所以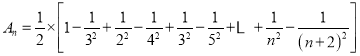
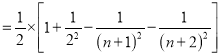

(4)第(3)问使用的是裂项相消法求数列的和,
![]() ;
;![]() ;
;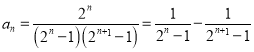 均适合该方法.
均适合该方法.

练习册系列答案
相关题目