题目内容
已知数列{an}满足a1= ,an=
,an=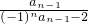 (n≥2,n∈N).
(n≥2,n∈N).
(1)试判断数列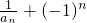 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设bn=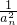 ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(3)设cn=ansin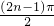 ,数列{cn}的前n项和为Tn.求证:对任意的n∈N*,Tn<
,数列{cn}的前n项和为Tn.求证:对任意的n∈N*,Tn< .
.
解:(1)∵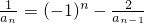 ,
,
∴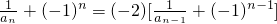 ,
,
又∵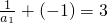 ,
,
∴数列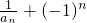 是首项为3,公比为-2的等比数列.
是首项为3,公比为-2的等比数列.
(2)依(1)的结论有 ,
,
即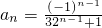 .
.
bn=(3•2n-1+1)2=9•4n-1+6•2n-1+1.
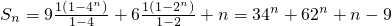 .
.
(3)∵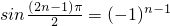 ,
,
∴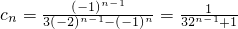 .
.
当n≥3时,
则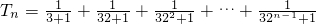 <
<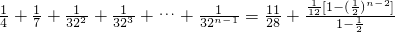
=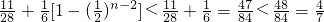 .
.
∵T1<T2<T3,
∴对任意的n∈N*,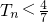 .
.
分析:(1)根据题意,对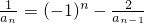 进行变形可得
进行变形可得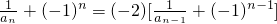 ,从而证得结论;
,从而证得结论;
(2)根据(1)求出数列an,从而求得bn,利用分组求和法即可求得结果;
(3)首先确定出数列{cn}的通项公式,利用放缩的思想将数列的每一项进行放缩,转化为特殊数列的求和问题达到证明不等式的目的.
点评:本题考查数列的递推公式确定数列的思想,根据递推公式确定出数列是否满足特殊数列的定义,考查学生的转化与化归思想.第(3)问考查学生的不等式放缩的技巧与方法,关键要将数列{cn}的每一项进行放缩转化为特殊数列从而达到求和证明的目的,属难题.
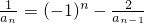 ,
,∴
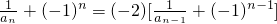 ,
,又∵
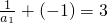 ,
,∴数列
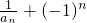 是首项为3,公比为-2的等比数列.
是首项为3,公比为-2的等比数列.(2)依(1)的结论有
 ,
,即
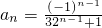 .
.bn=(3•2n-1+1)2=9•4n-1+6•2n-1+1.
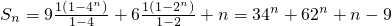 .
.(3)∵
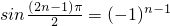 ,
,∴
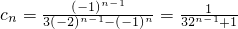 .
.当n≥3时,
则
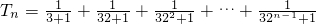 <
<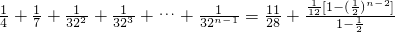
=
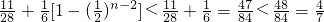 .
.∵T1<T2<T3,
∴对任意的n∈N*,
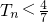 .
.分析:(1)根据题意,对
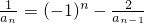 进行变形可得
进行变形可得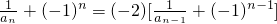 ,从而证得结论;
,从而证得结论;(2)根据(1)求出数列an,从而求得bn,利用分组求和法即可求得结果;
(3)首先确定出数列{cn}的通项公式,利用放缩的思想将数列的每一项进行放缩,转化为特殊数列的求和问题达到证明不等式的目的.
点评:本题考查数列的递推公式确定数列的思想,根据递推公式确定出数列是否满足特殊数列的定义,考查学生的转化与化归思想.第(3)问考查学生的不等式放缩的技巧与方法,关键要将数列{cn}的每一项进行放缩转化为特殊数列从而达到求和证明的目的,属难题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目