题目内容
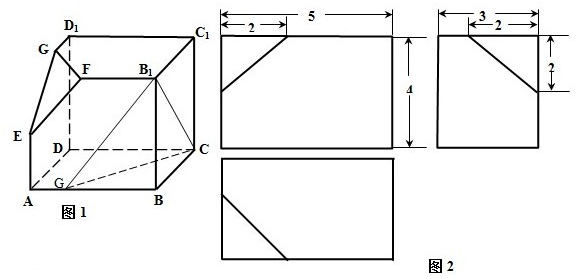
(2009•嘉定区二模)图1所示的是一个长方体截去一个角所得多面体的直观图.图2是它的主视图和左视图(单位:cm).
(1)在主视图下面按照三视图的要求画出该多面体的俯视图;
(2)按照图2给出的尺寸,求该多面体的体积;
(3)在图1中连接B1C,求异面直线EF和B1C所成角的大小(结果用反三角函数表示).

(1)在主视图下面按照三视图的要求画出该多面体的俯视图;
(2)按照图2给出的尺寸,求该多面体的体积;
(3)在图1中连接B1C,求异面直线EF和B1C所成角的大小(结果用反三角函数表示).
分析:(1)根据几何体的结构特征与它的正(主)视图和侧(左)视图可得其侧视图.
(2)由题意可得:所求多面体体积V=V长方体-V正三棱锥,
(3)在AB上取一点G,使AG=1(BG=4),连接B1G,CG,则∠FB1G=45°,所以B1G∥FE,所以∠CB1G(或其补角)就是异面直线EF和B1C所成的角.在△CB1G中 求解即可.
(2)由题意可得:所求多面体体积V=V长方体-V正三棱锥,
(3)在AB上取一点G,使AG=1(BG=4),连接B1G,CG,则∠FB1G=45°,所以B1G∥FE,所以∠CB1G(或其补角)就是异面直线EF和B1C所成的角.在△CB1G中 求解即可.
解答:解:(1)
注:正确作出图形得(3分),作错不给分.
(2)V=5×4×3-
×
×2×2×2=60-
=
(cm3),
所以,该多面体的体积为
cm3.…(8分)
(3)由已知,∠B1FE=135°,在AB上取一点G,使AG=1(BG=4),连接B1G,CG,则∠FB1G=45°,所以B1G∥FE,所以∠CB1G(或其补角)就是异面直线EF和B1C所成的角.…(10分)
在△CB1G中,B1G=4
,B1C=GC=5,所以cos∠CB1G=
.…(13分)
所以异面直线EF和B1C所成角的大小为arccos
.…(14分)

注:正确作出图形得(3分),作错不给分.
(2)V=5×4×3-
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 176 |
| 3 |
所以,该多面体的体积为
| 176 |
| 3 |
(3)由已知,∠B1FE=135°,在AB上取一点G,使AG=1(BG=4),连接B1G,CG,则∠FB1G=45°,所以B1G∥FE,所以∠CB1G(或其补角)就是异面直线EF和B1C所成的角.…(10分)
在△CB1G中,B1G=4
| 2 |
2
| ||
| 5 |
所以异面直线EF和B1C所成角的大小为arccos
2
| ||
| 5 |
点评:本题考查该多面体的三视图,多面体的体积的计算,异面直线所成角的大小计算,考查化归与转化(不规则几何体转化为规则几何体求体积、空间角转化为平面角)的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目