题目内容
11.已知数列{an}满足:a1=a2=1,且an2+an-1an+1=4an-1an(n∈N*,n≥2).(I)令bn=$\frac{{a}_{n+1}}{{a}_{n}}$(n∈N*),求数列{bn}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn.
分析 (I)通过计算出数列{an}前几项的值,猜想通项公式,进而利用数学归纳法证明即可;
(Ⅱ)通过(I)可知数列{an}的通项公式,进而分类讨论即得结论.
解答 解:(I)∵a1=a2=1,且an2+an-1an+1=4an-1an(n∈N*,n≥2),
∴a3=4-1=3,a4=12-9=3,a5=$\frac{36-9}{3}$=9,a6=$\frac{12×9-{9}^{2}}{3}$=9,
猜想:a2n-1=a2n=3n-1.
下面用数学归纳法来证明:
①当n=1时,显然命题成立;
②假设当n=k(k≥2)时,a2k-1=a2k=3k-1,
则a2k+1=$\frac{4{a}_{2k-1}{a}_{2k}-{{a}_{2k}}^{2}}{{a}_{2k-1}}$=$\frac{4•{3}^{k-1}•{3}^{k-1}-{3}^{k-1}•{3}^{k-1}}{{3}^{k-1}}$=3k,
a2k+2=$\frac{4{a}_{2k}{a}_{2k+1}-{{a}_{2k+1}}^{2}}{{a}_{2k}}$=$\frac{4•{3}^{k-1}•{3}^{k}-{3}^{k}•{3}^{k}}{{3}^{k-1}}$=3k,
即当n=k+1时,命题成立;
由①②可知,a2n-1=a2n=3n-1.
∴bn=$\frac{{a}_{n+1}}{{a}_{n}}$=$\left\{\begin{array}{l}{1,}&{n为奇数}\\{3,}&{n为偶数}\end{array}\right.$(n∈N*);
(Ⅱ)由(I)可知,an=$\left\{\begin{array}{l}{{3}^{\frac{n-1}{2}},}&{n为奇数}\\{{3}^{\frac{n-2}{2}},}&{n为偶数}\end{array}\right.$,
∴当n为偶数时,Sn=2•$\frac{1-{3}^{\frac{n}{2}}}{1-3}$=${3}^{\frac{n}{2}}$-1;
当n为奇数时,Sn=Sn+1-an+1=2•$\frac{1-{3}^{\frac{n+1}{2}}}{1-3}$-${3}^{\frac{n-1}{2}}$=${3}^{\frac{n+1}{2}}$-${3}^{\frac{n-1}{2}}$-1;
综上所述,Sn=$\left\{\begin{array}{l}{{3}^{\frac{n+1}{2}}-{3}^{\frac{n-1}{2}}-1,}&{n为奇数}\\{{3}^{\frac{n}{2}}-1,}&{n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查数学归纳法,考查分类讨论的思想,注意解题方法的积累,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
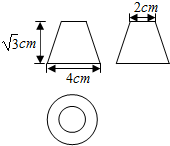
| A. | $\frac{{7\sqrt{3}π}}{3}$ | B. | $\frac{{8\sqrt{3}π}}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |