题目内容
8.函数y=x2一点P(非原点),在P处引切线交x轴,y轴于Q,R,求$\frac{|PQ|}{|PR|}$.分析 如图所示,设切点P$({x}_{0},{x}_{0}^{2})$,利用导数的几何可得切线的斜率,得到切线方程,即可得出点Q,R的坐标.即可得出.
解答 解:如图所示,
设切点P$({x}_{0},{x}_{0}^{2})$,
∵y′=2x,
∴切线的斜率为:k=2x0,
∴切线方程为:$y-{x}_{0}^{2}=2{x}_{0}(x-{x}_{0})$,
令y=0,可得x=$\frac{{x}_{0}}{2}$,∴Q$(\frac{{x}_{0}}{2},0)$;
令x=0,可得$y=-{x}_{0}^{2}$,∴R$(0,-{x}_{0}^{2})$.
可知:Q点为线段PR的中点,
∴$\frac{|PQ|}{|PR|}$=$\frac{1}{2}$.
点评 本题考查了导数的几何意义、抛物线的切线方程、中点坐标公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | “x<0”是“ln(x+1)<0”的充要条件 | |
| B. | “?x≥2,x2-3x+2≥0”的否定是“?x<2,x2-3x+2<0” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8 |
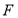 是抛物线
是抛物线 的焦点,
的焦点, 是
是 上的两个点,线段
上的两个点,线段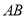 的中点为
的中点为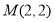 ,则
,则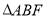 的面积等于 .
的面积等于 . 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小. 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.