题目内容
16. 如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
如图,四棱锥P-ABCD中底面是变长为a的正方形,且PD=a,PA=PC=$\sqrt{2}a$,求平面APB与平面PBD夹角的大小.
分析 过点O作OE⊥PB于点E,连接AE,说明∠AEO是二面角A-PB-D的平面角,在Rt△AEO中,可求二面角A-PB-D的大小.
解答  解:过点O作OE⊥PB于点E,连接AE.
解:过点O作OE⊥PB于点E,连接AE.
∵AO⊥平面PBD,∴由三垂线定理得AE⊥PB.
∴∠AEO是二面角A-PB-D的平面角.
∵PD⊥平面ABCD,∴AD⊥AB,由三垂线定理得PA⊥AB.
在Rt△PAB中,PB=$\sqrt{3}$a,
∴AE=$\frac{PA•AB}{PB}$=$\frac{\sqrt{6}}{3}$.
∴在Rt△AEO中,sin∠AEO=$\frac{AO}{AE}$=$\frac{\sqrt{3}}{2}$.
∴二面角A-PB-D的大小为60°.
点评 本题考查线面垂直,二面角的作法以及求解方法,考查空间想象能力以及计算能力.,

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.已知M(2,4)是抛物线y2=8x上一定点,A,B是抛物线上异于M的两个动点,若MA⊥MB,直线AB必过的定点的坐标为( )
| A. | (8,-4) | B. | (10,-4) | C. | (10,4) | D. | (8,4) |
 的图象不过原点,且关于原点对称,则
的图象不过原点,且关于原点对称,则 的取值是( )
的取值是( )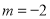 B.
B.
 或
或 D.
D.
 如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.
如图,过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1,求证:FM⊥FN.