题目内容
已知椭圆的中心在原点,离心率 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为
 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为A.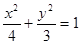 | B. | C. | D. |
A
试题分析:抛物线
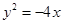 焦点为
焦点为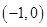 ,所以椭圆中
,所以椭圆中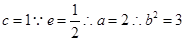 ,方程为
,方程为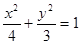
点评:抛物线
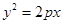 的焦点为
的焦点为 ,椭圆
,椭圆 中
中 ,离心率
,离心率

练习册系列答案
相关题目
题目内容
 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合, 则此椭圆方程为
的焦点重合, 则此椭圆方程为A.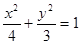 | B. | C. | D. |
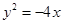 焦点为
焦点为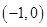 ,所以椭圆中
,所以椭圆中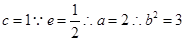 ,方程为
,方程为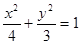
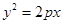 的焦点为
的焦点为 ,椭圆
,椭圆 中
中 ,离心率
,离心率
