题目内容
9.已知函数f(x)对任意实数x,y满足f(x+y)=f(x)+f(y),且f(1)≥2.若存在整数m,使得f(-2)-m2-m+4=0,则m取值的集合为{-1,0}.分析 根据抽象函数,判断函数的奇偶性,结合一元二次不等式的性质进行求解即可.
解答 解:令x=y=0得f(0)=f(0)+f(0),
解得f(0)=0,
令y=-x,则f(x-x)=f(x)+f(-x)=f(0)=0,
即f(-x)=-f(x),
∴函数f(x)是奇函数,
若存在整数m,使得f(-2)-m2-m+4=0,
则-f(2)-m2-m+4=0,
即f(2)=-m2-m+4=-(m+$\frac{1}{2}$)2+$\frac{5}{4}$,
令x=y=1,则f(1+1)=f(1)+f(1),
即f(2)=2f(1)≥4,
即-m2-m+4≥4,
即-m2-m≥0.
则m2+m≤0,
解得-1≤m≤0,
∵m是整数,∴m=-1或0,
故m取值的集合为{-1,0},
故答案为:{-1,0}.
点评 本题主要考查抽象函数的应用,根据条件判断函数的奇偶性是解决本题的关键.综合考查函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.口袋中有20个球,其中白球9个,红球5个,黑球6个,现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是( )
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
17.已知某几何体的三视图如图所示,其中俯视图是扇形,则该几何体的体积为( )
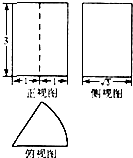

| A. | 4 π | B. | 2 π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
1.已知椭圆M:$\frac{{x}^{2}}{4}$+y2=1的上、下顶点为A,B,过点P(0,2)的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间),则$\overrightarrow{OC}$•$\overrightarrow{OD}$的取值范围( )
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |