题目内容
【题目】
已知等差数列![]() 的公差为
的公差为![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 与前
与前![]() 项和
项和![]() ;
;
(2)将数列![]() 的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列
的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列![]() 的前三项,记数列
的前三项,记数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在
,若存在![]() ,使得对任意
,使得对任意![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]()
![]() (2)
(2)![]()
【解析】
试题(1)求等差数列通项公式,一般利用待定系数法,本题已知公差,因此只需确定一项即可:由![]() 利用等差数列性质得
利用等差数列性质得![]() ,
,![]() ,再根据等差数列广义通项公式得:
,再根据等差数列广义通项公式得:![]() ,最后利用等差数列和项公式求前
,最后利用等差数列和项公式求前![]() 项和
项和![]() ,(2)先根据题意确定数列
,(2)先根据题意确定数列![]() 的前四项抽取的是哪一项,再根据剩下三项,利用待定系数法求等比数列
的前四项抽取的是哪一项,再根据剩下三项,利用待定系数法求等比数列![]() 通项,然后利用错位相减法求数列
通项,然后利用错位相减法求数列![]() 的前
的前![]() 项和为
项和为![]() ,对存在性问题及恒成立问题,一般转化为对应函数最值问题:
,对存在性问题及恒成立问题,一般转化为对应函数最值问题:![]() ,
,![]() 为二次函数,可根据对称轴求其最大值,需注意
为二次函数,可根据对称轴求其最大值,需注意![]() ,而
,而![]() 的最值,需根据数列单调性确定.
的最值,需根据数列单调性确定.
试题解析:
解:(1)![]()
![]() 为等差数列,且
为等差数列,且![]() ,
,![]()
![]() ,即
,即![]() ,
,
又![]() 公差
公差![]() ,
,![]()
![]() ,
,![]() .
.
![]() ,
,![]() .
.
(2)由(1)知数列![]() 的前
的前![]() 项为
项为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 等比数列
等比数列![]() 的前
的前![]() 项为
项为![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
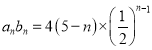 ,
,
![]()
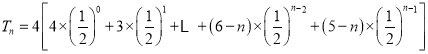 ,①
,①
![]()
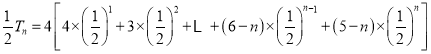 ,②
,②
①![]() ②得
②得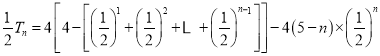
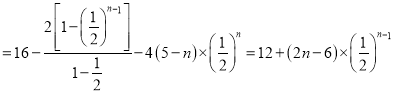 .
.
![]()
![]() ,
,![]() .
.
![]()
![]() ,
,
![]()
![]() ,且
,且![]() ,
,
![]()
![]() 时,
时,![]() .
.
又![]()
![]() ,
,
![]()
![]() 时,
时,![]() ,
,
![]() 存在
存在![]() ,使得对任意
,使得对任意![]() ,总有
,总有![]() 成立.
成立.
![]()
![]() ,
,![]()
![]() ,
,
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
【题目】为考察某种疫苗预防疾病的效果,进行动物试验,得到统计数据如下:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 40 | y | B |
总计 | 60 | 40 | 100 |
(1)求2×2列联表中的数据x,y,A,B的值.
(2)能否在犯错误的概率不超过0.01的前提下认为疫苗有效?
附:![]()
临界值表:
P(K2≥k0) | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |