题目内容
在一次购物抽奖活动中,假设某6张券中有一等奖 券1张,可获价值50元的奖品;有二等奖券1张,每张可获价值20元的奖品;其余4张没有奖.某顾客从此6张中任抽1张,求:
(1)该顾客中奖的概率;
(2)该顾客参加此活动可能获得的奖品价值的期望值.
(1)该顾客中奖的概率;
(2)该顾客参加此活动可能获得的奖品价值的期望值.
(1) ,(2)
,(2)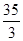 元.
元.
 ,(2)
,(2)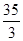 元.
元.试题分析:(1)
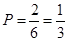 ,
,即该顾客中奖的概率为1/3. 3分
(2)
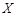 的所有可能值为:0,20,50(元), …….4分
的所有可能值为:0,20,50(元), …….4分且
 ,
, ,
,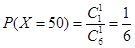 , 7分
, 7分故
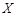 的分布列为
的分布列为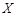 | 0 | 20 | 50 |
 | 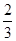 | 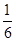 | 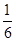 |
E(X)=
 =
=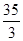 ,
,所以该顾客参加此活动可能获得奖品价值的期望值是
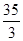 元. 10分
元. 10分点评:求解有关概率问题时,首先要能够根据题意确定基本事件空间,而后确定事件所含的基本事件个数,则对应的概率值可求。在确定基本事件空间和事件A包含的基本事件个数时,要注意计算的准确性,做到不重不漏,求解分布列问题时,注意分布列的性质的运用。

练习册系列答案
相关题目
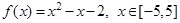 ,若从区间
,若从区间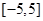 内随机选取一个实数
内随机选取一个实数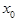 ,则所选取的实数
,则所选取的实数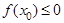 的概率为( )
的概率为( )  .已知该足球队进行一场比赛得分的期望是1, 则
.已知该足球队进行一场比赛得分的期望是1, 则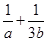 的最小值为( )
的最小值为( )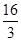
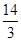
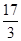
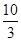
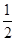 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.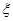 和
和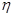 ,其中
,其中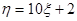 ,且
,且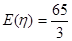 ,若
,若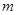 的值为
的值为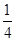
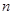
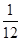
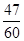 B.
B.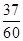 C.
C.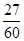 D.
D.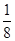
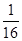
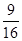
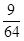
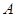 、
、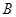 两名教师被同时分配到甲学校的概率;
两名教师被同时分配到甲学校的概率;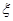 为这四名教师中分配到甲学校的人数,求
为这四名教师中分配到甲学校的人数,求 ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.