题目内容
1.在数列{an}中,如果an+1=$\frac{{a}_{n}+{a}_{n+2}}{2}$对任意的n∈N*都成立,求证数列{an}是等差数列.分析 根据等差数列的定义进行判断和证明即可.
解答 证明:∵an+1=$\frac{{a}_{n}+{a}_{n+2}}{2}$,
∴2an+1=an+an+2,
即an+1-an=an+2-an+1,
即数列{an}是等差数列.
点评 本题主要考查等差数列的判断,根据等差数列的定义是解决本题的关键.

练习册系列答案
相关题目
12.一个底面直径等于高的圆柱的轴截面面积是S,则它的一个底面面积是( )
| A. | $\frac{π}{2}$S | B. | $\frac{π}{4}$S | C. | S | D. | πS |
13.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D.则四面体ABCD的四个顶点所在球的半径为( )
| A. | $\frac{5}{2}$ | B. | $\frac{25}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{25}$ |
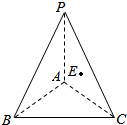 已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.
已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.