一个棱台被平行于底面的平面所截.若上底底面面积.截面面积与下底底面面积之比为4:9:16.则此棱台的侧棱被分成上下两部分之比为1:1．题目和参考答案——青夏教育精英家教网—

题目内容

3．一个棱台被平行于底面的平面所截，若上底底面面积、截面面积与下底底面面积之比为4：9：16，则此棱台的侧棱被分成上下两部分之比为1：1．

分析由截面与底面为相似多边形，可得三棱锥侧棱之比为2：3：4，原棱锥的侧棱被分成的比为2：1：1，即可得出结论．

解答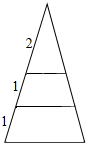解：根据还台于锥的办法可得，由截面与底面为相似多边形，且上底底面面积、截面面积与下底底面面积之比为4：9：16，
∴三棱锥侧棱之比为2：3：4，
∴原棱锥的侧棱被分成的比为2：1：1
此棱台的侧棱被分成上下两部分之比为1：1．
故答案为：1：1，

点评本题考查的知识点是棱锥的几何特征，其中根据相似的性质，及截面面积与底面面积之比得到相似比是解答的关键．

一题一题找答案解析太慢了
下载作业精灵直接查看整书答案解析立即下载

练习册系列答案

相关题目

2．

如图，某渔船在航行中不幸遇险，发出呼救信号，我海军舰在A处获悉后，测出该渔船在方位角为30°、距离为10海里的C处，并测得该渔船正沿方位角为90°的方向，以30海里/时的速度向小岛P靠拢，我海军舰立即以30

\sqrt{3}

$\sqrt{3}$ 海里/时的速度前去营救，求舰艇的航向和靠近渔船所需的时间（注：方位角是从指北方向顺时针转到目标方向线的角）．

3．已知两个等差数列5，8，11和3，7，11都有100项，它们的共同项之和为3875．

20．求使下列函数取得最大值、最小值的自变量x的集合，并分别写出最大值和最小值：
（1）y=-3sinx，x∈R；
（2）y=2+cos

\frac{x}{2}

$\frac{x}{2}$ ，x∈R；
（3）y=-

\frac{1}{2}

$\frac{1}{2}$ sin（3x+

\frac{π}{4}

$\frac{π}{4}$ ），x∈R．

7．计算：

\frac{c o s （ α - \frac{π}{2} ）}{s i n （ α + \frac{5 π}{2} ）}

$\frac{cos（α-\frac{π}{2}）}{sin（α+\frac{5π}{2}）}$ -sin（α-π）cos（π-α）．

8．

如图所示，在正方体ABCD-A₁B₁C₁D₁中，E为DD₁上一点，且DE=

\frac{1}{3}

$\frac{1}{3}$ DD₁，F是侧面CDD₁C₁上的动点，且B₁F∥平面A₁BE，则B₁F与平面CDD₁C₁所成角的正切值构成的集合是（　　）

A．

{

\frac{3}{2}

$\frac{3}{2}$ }

B．

{

\frac{2}{5} \sqrt{13}

$\frac{2}{5}\sqrt{13}$ }

C．

{m|

\frac{3}{2}

$\frac{3}{2}$ ≤m≤

\frac{3}{2}

$\frac{3}{2}$

\sqrt{2}

$\sqrt{2}$ }

D．

{m|

\frac{2}{5}

$\frac{2}{5}$

\sqrt{13}

$\sqrt{13}$ ≤m≤

\frac{3}{2}

$\frac{3}{2}$ }

15．若AB为经过抛物线y²=4x焦点的弦，且AB=4，O为坐标原点，则△OAB的面积等于2．

12．已知抛物线

x = \frac{1}{2} y^{2}

$x=\frac{1}{2}{y^2}$ 上一点P的横坐标为1，则点P到该抛物线的焦点F的距离为（　　）

A．

\frac{9}{8}

$\frac{9}{8}$

B．

\frac{3}{2}

$\frac{3}{2}$

C．

D．

\frac{5}{4}

$\frac{5}{4}$

13．已知数列{a_n}为等比数列，b_n=log

_{\frac{1}{2}}

${\;}_{\frac{1}{2}}$ a_n，b₂+b₄=12，b₃+b₅=16．
（1）求{b_n}的通项公式；
（2）求{b_n}的前100项和．

试题分类