题目内容
【题目】如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=![]() ,点E在A1D上
,点E在A1D上
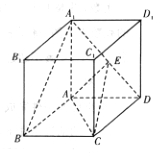
(1)求证:AA1⊥平面ABCD;
(2)当E为线段A1D的中点时,求点A1到平面EAC的距离
【答案】(1)见证明;(2)![]()
【解析】
(1)根据题中所给的数据,由勾股定理得![]() 由线面垂直的判定定理即得到证明;(2)设
由线面垂直的判定定理即得到证明;(2)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,当E为A1D的中点时,可得
,当E为A1D的中点时,可得![]() 平面
平面![]() ,得点
,得点![]() 到面
到面![]() 的距离可转为点
的距离可转为点![]() 到平面
到平面![]() 的距离,然后利用等体积转化即可得到答案.
的距离,然后利用等体积转化即可得到答案.
(1)证明:![]() 底面
底面![]() 是菱形,
是菱形,![]()
在![]() 中,由
中,由![]() 知
知![]() ,
,
同理,![]() ,
,
又![]() 平面
平面![]() .
.
(2)解:设![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的中点时,连接
的中点时,连接![]() ,
,
则![]() 平面
平面![]() ,
,
直线![]() 与平面
与平面![]() 之间的距离等于点
之间的距离等于点![]() 到平面
到平面![]() 的距离,可转化为点
的距离,可转化为点![]() 到平面
到平面![]() 的距离,
的距离,

过点![]() 作
作![]() 于
于![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() , 又
, 又![]() ,
,
![]() ,
,
设![]() 表示点
表示点![]() 到平面
到平面![]() 的距离,则
的距离,则![]() ,
,
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]()

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目