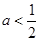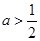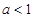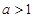题目内容
设f(x)=|x-3|+|x-4|.
(1)解不等式f(x)≤2;
(2)若存在实数x满足f(x)≤ax-1,试求实数a的取值范围.
(1)解不等式f(x)≤2;
(2)若存在实数x满足f(x)≤ax-1,试求实数a的取值范围.
解(1)f(x)=|x-3|+|x-4|=
,
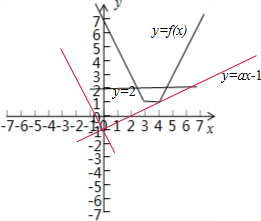
由图象可得f(x)≤2的解集为[
,
]-(5分)
(2)函数y=ax-1,的图象是经过点(0,-1)的直线,
由图象可得a∈(-∞,-2)∪[
,+∞)-----(10分)
|
由图象可得f(x)≤2的解集为[
| 5 |
| 2 |
| 9 |
| 2 |
(2)函数y=ax-1,的图象是经过点(0,-1)的直线,
由图象可得a∈(-∞,-2)∪[
| 1 |
| 2 |


练习册系列答案
相关题目
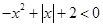 的解集是
的解集是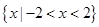

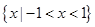
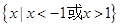
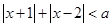 无实数解,则
无实数解,则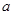 的取值范围是 .
的取值范围是 .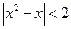 的解集为()
的解集为()
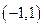
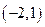
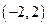
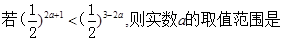 ( )
( )