题目内容
a、b∈R,“a≠b”是“a2+b2>2ab”成立的( )
| A.充要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
∵a2+b2-2ab=(a-b)2,
∴若a≠b,则a2+b2-2ab=(a-b)2>0,即a2+b2>2ab成立.
若a2+b2>2ab,
则a2+b2-2ab=(a-b)2>0,
∴a≠b,
∴“a≠b”是“a2+b2>2ab”成立的充要条件.
故选:A.
∴若a≠b,则a2+b2-2ab=(a-b)2>0,即a2+b2>2ab成立.
若a2+b2>2ab,
则a2+b2-2ab=(a-b)2>0,
∴a≠b,
∴“a≠b”是“a2+b2>2ab”成立的充要条件.
故选:A.

练习册系列答案
相关题目
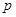 :“方程
:“方程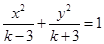 表示双曲线”(
表示双曲线”(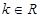 );命题
);命题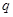 :
: 定义域为
定义域为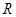 .若命题
.若命题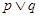 为真命题,
为真命题,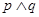 为假命题,求实数
为假命题,求实数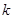 的取值范围.
的取值范围.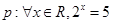 ,则
,则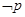 为( )
为( )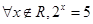
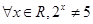
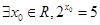
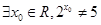
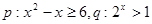 ,若
,若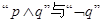 同时为假命题,求x的取值集合.
同时为假命题,求x的取值集合.