题目内容
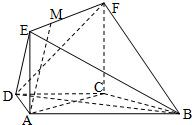 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.(Ⅰ)求证:BC⊥平面ACFE;.
(Ⅱ)求二面角B-EF-D的平面角的余弦值.
分析:(Ⅰ)欲证BC⊥平面ACFE,可根据面面垂直的性质定理进行证明,而AC⊥BC,平面ACFE⊥平面ABCD,交线为AC,满足面面垂直的性质定理;
(Ⅱ)取EF中点G,EB中点H,连接DG,GH,DH,根据二面角的平面角的定义可知∠DGH是二面角B-EF-D的平面角,在△DGH中,利用余弦定理即可求出二面角B-EF-D的平面角的余弦值.
(Ⅱ)取EF中点G,EB中点H,连接DG,GH,DH,根据二面角的平面角的定义可知∠DGH是二面角B-EF-D的平面角,在△DGH中,利用余弦定理即可求出二面角B-EF-D的平面角的余弦值.
解答: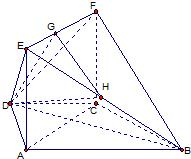 解(Ⅰ)在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°
解(Ⅰ)在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°∴AC⊥BC(3分)
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE(5分)
(Ⅱ)取EF中点G,EB中点H,连接DG,GH,DH∵DE=DF,
∴DG⊥EF∵BC⊥平面ACFE∴BC⊥EF
又∵EF⊥FC,∴EF⊥FB,
又∵GH∥FB,
∴EF⊥GH
∴BE2=DE2+DB2∴∠DGH是二面角B-EF-D的平面角.(8分)
在△BDE中,DE=
a,DB=
a,BE=
=
a∴∠EDB=90°,
∴DH=
a.(9分)
又DG=
a,GH=
a.(10分)
即二面角B-EF-D的平面角的余弦值为
 解(Ⅰ)在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°
解(Ⅰ)在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°∴AC⊥BC(3分)
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE(5分)
(Ⅱ)取EF中点G,EB中点H,连接DG,GH,DH∵DE=DF,
∴DG⊥EF∵BC⊥平面ACFE∴BC⊥EF
又∵EF⊥FC,∴EF⊥FB,
又∵GH∥FB,
∴EF⊥GH
∴BE2=DE2+DB2∴∠DGH是二面角B-EF-D的平面角.(8分)
在△BDE中,DE=
| 2 |
| 3 |
| AE2+AB2 |
| 5 |
∴DH=
| ||
| 2 |
又DG=
| ||
| 2 |
| ||
| 2 |
即二面角B-EF-D的平面角的余弦值为
| ||
| 10 |
点评:本题主要考查了直线与平面垂直的判定,以及与二面角有关的立体几何综合题,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
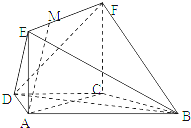 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.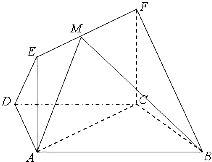 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.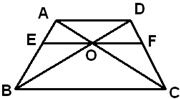 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.