题目内容
若函数
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,求函数
时,求函数 的值域.
的值域.

(Ⅰ)求函数
 的单调递增区间;
的单调递增区间;(Ⅱ)当
 时,求函数
时,求函数 的值域.
的值域.(Ⅰ) 的单调递增区间为
的单调递增区间为
(2) 的值域为
的值域为 .
.
 的单调递增区间为
的单调递增区间为
(2)
 的值域为
的值域为 .
.(Ⅰ)先利用二倍角公式及两角和差正弦公式化简三角函数,然后代入正弦函数的递增区间求解即可;(Ⅱ)先求出角的范围,然后利用单调性求出函数的值域
(Ⅰ)
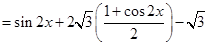


 3分
3分
由 解得
解得
所以函数 的单调递增区间为
的单调递增区间为 5分
5分
(2)当 时,则
时,则 ,则
,则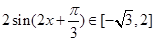
所以函数 的值域为
的值域为
(Ⅰ)

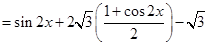


 3分
3分由
 解得
解得
所以函数
 的单调递增区间为
的单调递增区间为 5分
5分(2)当
 时,则
时,则 ,则
,则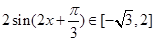
所以函数
 的值域为
的值域为

练习册系列答案
相关题目

 的图象的一段,其解析式为 ;
的图象的一段,其解析式为 ;
 4sin x
4sin x 的部分图像如右图所示,设
的部分图像如右图所示,设 是图像的一个最高点,
是图像的一个最高点, 是图像与
是图像与 轴的交点,若
轴的交点,若 ,则
,则


 ,
, .
. 时,求函数
时,求函数 ,
, ,则
,则 是( )
是( ) 的奇函数
的奇函数 的奇函数
的奇函数 的值为 .
的值为 . ,若
,若 ,则
,则 的取值范围是 。
的取值范围是 。