题目内容
已知 ,
, R
R
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 恒成立,求k的取值范围.
恒成立,求k的取值范围.
 ,
, R
R(Ⅰ)当
 时,解不等式
时,解不等式 ;
;(Ⅱ)若
 恒成立,求k的取值范围.
恒成立,求k的取值范围.(Ⅰ){x|x>-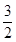 };(Ⅱ)[12,+∞).
};(Ⅱ)[12,+∞).
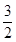 };(Ⅱ)[12,+∞).
};(Ⅱ)[12,+∞). 试题分析:(Ⅰ)利用分类讨论思想将函数转化为分段函数,然后逐一求解每个不等式;(Ⅱ)利用绝对值性质定理求解f(x)=|ax-4|-|ax+8|的最大值,然后确定k的取值范围.
试题解析:(Ⅰ)当a=2时,
f(x)=2(|x-2|-|x+4|)=
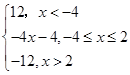
当x<-4时,不等式不成立;
当-4≤x≤2时,由-4x-4<2,得-
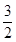 <x≤2;
<x≤2;当x>2时,不等式必成立.
综上,不等式f(x)<2的解集为{x|x>-
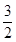 }.
}.(Ⅱ)因为f(x)=|ax-4|-|ax+8|≤|(ax-4)-(ax+8)|=12,
当且仅当ax≤-8时取等号.
所以f(x)的最大值为12.
故k的取值范围是[12,+∞).

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

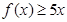 ;
;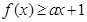 的解集为
的解集为 ,求实数
,求实数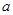 的取值范围
的取值范围 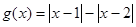 ,则
,则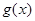 的值域为 ;若关于
的值域为 ;若关于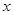 的不等式
的不等式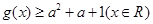 的解集为空集,则实数
的解集为空集,则实数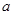 的取值范围是 .
的取值范围是 .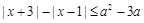 对任意实数
对任意实数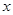 恒成立,则实数
恒成立,则实数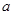 的取值范围为( )
的取值范围为( )
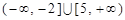

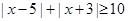 的解集为
的解集为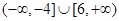
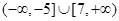
 的解集为
的解集为  的不等式
的不等式 ,其中
,其中 是实参数.
是实参数. 时,解上面的不等式.
时,解上面的不等式. ,上面的不等式均成立,求实数
,上面的不等式均成立,求实数 的解集为
的解集为 ,则实数
,则实数 的取值范围是____.
的取值范围是____.