Question

16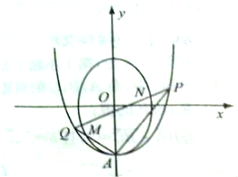．如图，过抛物线C₁：y=$\frac{1}{4}$x²-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线，与抛物线交于另两点P、Q直线（PQ不与x轴垂直）与椭圆C₂：$\frac{{y}^{2}}{4}$+x²=1相交于点M、N．
（1）若直线PQ与y轴交于点T（0，t），求t的值；
（2）若直线PQ，AM，AN的斜率分别为k，k₁，k₂，且k＞0，求$\frac{1}{k}$-$\frac{1}{{k}_{1}}$-$\frac{1}{{k}_{2}}$的最小值．

Answer 1

分析 （1）A（0，-2），设直线AP的斜率为k≠0，则直线AQ的斜率为：-$\frac{1}{4k}$．可得直线AP，AQ的方程分别为：y=kx-2，y=-$\frac{1}{4k}$x-2，分别与抛物线方程联立可得P，Q的坐标，利用点斜式可得直线PQ的方程，令x=0，即可解出t．
（2）设M（x₁，y₁），N（x₂，y₂），直线PQ的方程为：y=kx-1，与椭圆方程联立化为（4+k²）x²-2kx-3=0，可得根与系数的关系，利用斜率计算公式可得：k_AM=$\frac{{y}_{1+2}}{{x}_{1}}$=$\frac{k{x}_{1}+1}{{x}_{1}}$=k₁，k_AN=$\frac{k{x}_{2}+1}{{x}_{2}}$=k₂．代入$\frac{1}{k}$-$\frac{1}{{k}_{1}}$-$\frac{1}{{k}_{2}}$=$\frac{1}{k}$-$\frac{{x}_{1}}{k{x}_{1}+1}$-$\frac{{x}_{2}}{k{x}_{2}+1}$，化简整理再利用基本不等式的性质即可得出．

解答 解：（1）A（0，-2），设直线AP的斜率为k≠0，则直线AQ的斜率为：-$\frac{1}{4k}$．
可得直线AP，AQ的方程分别为：y=kx-2，y=-$\frac{1}{4k}$x-2，
联立$\left\{\begin{array}{l}{y=kx-2}\\{y=\frac{1}{4}{x}^{2}-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=4k}\\{y=4{k}^{2}-2}\end{array}\right.$，∴P（4k，4k²-2）．
同理可得Q$（-\frac{1}{k}，\frac{1}{4{k}^{2}}-2）$．
∴直线PQ的方程为：$y-（4{k}^{2}-2）=\frac{4{k}^{2}-2-（\frac{1}{4{k}^{2}}-2）}{4k+\frac{1}{k}}$（x-4k），
令x=0，化为y+2=1，解得y=-1，
∴t=-1，∴直线PQ与y轴交于点T（0，-1）．
（2）设M（x₁，y₁），N（x₂，y₂），直线PQ的方程为：y=kx-1，
联立$\left\{\begin{array}{l}{y=kx-1}\\{\frac{{y}^{2}}{4}+{x}^{2}=1}\end{array}\right.$，化为（4+k²）x²-2kx-3=0，
∴x₁+x₂=$\frac{2k}{4+{k}^{2}}$，x₁x₂=$\frac{-3}{4+{k}^{2}}$．
k_AM=$\frac{{y}_{1+2}}{{x}_{1}}$=$\frac{k{x}_{1}+1}{{x}_{1}}$=k₁，k_AN=$\frac{k{x}_{2}+1}{{x}_{2}}$=k₂．
∵k＞0，
∴$\frac{1}{k}$-$\frac{1}{{k}_{1}}$-$\frac{1}{{k}_{2}}$=$\frac{1}{k}$-$\frac{{x}_{1}}{k{x}_{1}+1}$-$\frac{{x}_{2}}{k{x}_{2}+1}$=$\frac{1}{k}$-$\frac{2k{x}_{1}{x}_{2}+（{x}_{1}+{x}_{2}）}{{k}^{2}{x}_{1}{x}_{2}+k（{x}_{1}+{x}_{2}）+1}$=$\frac{1}{k}$+k≥2，当且仅当k=1时，取等号．
∴$\frac{1}{k}$-$\frac{1}{{k}_{1}}$-$\frac{1}{{k}_{2}}$的最小值为2．

点评 本题考查了抛物线标准方程及其性质、直线与抛物线相交转化为方程联立可得可得根与系数的关系、斜率计算公式，考查了推理能力与计算能力，属于中档题．