题目内容
5.若复数z=5cosα-4•i(i为虚数单位,-π<α<0)在复平面上的对应点在直线y=x-1上,则sinα=$-\frac{4}{5}$.分析 由复数z=5cosα-4•i在复平面上的对应点在直线y=x-1上列式求得cosα=-$\frac{3}{5}$,再由α的范围结合同角三角函数的基本关系式得答案.
解答 解:∵复数z=5cosα-4•i在复平面上的对应点在直线y=x-1上,
∴-4=5cosα-1,即cosα=-$\frac{3}{5}$,
又-π<α<0,∴$sinα=-\sqrt{1-co{s}^{2}α}=-\sqrt{1-(-\frac{3}{5})^{2}}=-\frac{4}{5}$.
故答案为:$-\frac{4}{5}$.
点评 本题考查了复数的代数表示法及其几何意义,考查了三角函数的求值,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知抛物线的方程为y2=4x,过其焦点F的直线与抛物线交于A、B两点,且|AF|=3,O为坐标原点,则△AOF的面积和△BOF的面积之比为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
17.设i是虚数单位,$\overline{z}$是复数z的共轭复数,若(1-i)$\overline{z}$=2,则z为( )
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
14.设全集为R,集合A={x∈R|x2<4},B={x|-1<x≤4},则A∩(∁RB)=( )
| A. | (-1,2) | B. | (-2,-1) | C. | (-2,-1] | D. | (-2,2) |
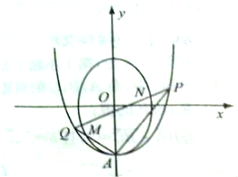 如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.
如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.