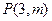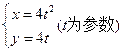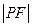题目内容
已知圆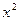 +
+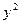 -9x=0,与顶点在原点,焦点在x轴上的抛物线交于A、B两点,
-9x=0,与顶点在原点,焦点在x轴上的抛物线交于A、B两点,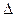 OAB的垂心恰为抛物线的焦点,求抛物线的方程。
OAB的垂心恰为抛物线的焦点,求抛物线的方程。
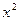 +
+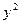 -9x=0,与顶点在原点,焦点在x轴上的抛物线交于A、B两点,
-9x=0,与顶点在原点,焦点在x轴上的抛物线交于A、B两点, OAB的垂心恰为抛物线的焦点,求抛物线的方程。
OAB的垂心恰为抛物线的焦点,求抛物线的方程。抛物线的方程为y2=4x
依题意,设所求抛物线方程为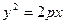 (
(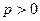 ),焦点F(
),焦点F(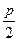 ,0),A(
,0),A(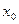 ,
,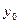 ),
),
B(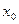 ,-
,-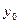 ),则
),则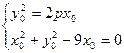 ,∴
,∴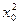 +(2p-9)
+(2p-9)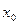 ="0 " ① ∵OA
="0 " ① ∵OA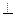 BF
BF
∴ ·
·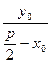 =-1 ,即
=-1 ,即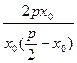 =-1,∴
=-1,∴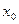 =
= ②
②
把②代入①得p="2," ∴所求抛物线的方程为y2=4x。
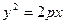 (
(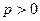 ),焦点F(
),焦点F(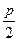 ,0),A(
,0),A(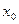 ,
,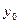 ),
),B(
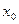 ,-
,-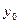 ),则
),则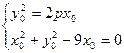 ,∴
,∴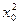 +(2p-9)
+(2p-9)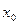 ="0 " ① ∵OA
="0 " ① ∵OA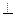 BF
BF ∴
 ·
·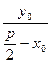 =-1 ,即
=-1 ,即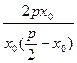 =-1,∴
=-1,∴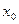 =
= ②
②把②代入①得p="2," ∴所求抛物线的方程为y2=4x。

练习册系列答案
相关题目
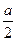 ,0)
,0)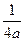 )
)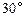 角,水流的最高点比喷头高出1.5米,用这种喷水器一次能灌溉多大面积.(精确到十位)
角,水流的最高点比喷头高出1.5米,用这种喷水器一次能灌溉多大面积.(精确到十位)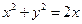 及抛物线S:
及抛物线S: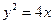 ,过圆心
,过圆心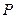 作直线
作直线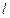 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为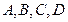 ,如果线段
,如果线段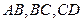 的长按此顺序构成一个等差数列,求直线l的方程.
的长按此顺序构成一个等差数列,求直线l的方程.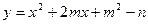 焦点坐标为(2001,2002),则它的顶点坐标为
焦点坐标为(2001,2002),则它的顶点坐标为 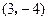 抛物线的标准方程。
抛物线的标准方程。