题目内容
直线l过抛物线y2=2px(p＞0）的焦点且与抛物线有两个交点，对于抛物线上另外两点A、B直线l能否平分线段AB？试证明你的结论.
直线l不能垂直平分线段AB
如果直线l垂直平分线段AB，连AF、BF，∵F（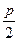
，0）∈l. ∴|FA|=|FB|,设A（x1,y1）,B(x2,y2),显然x1>0,x2>0,y1≠y2,
于是有（x1–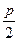）2+y12=(x2–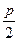)2+y22,
整理得:（x1+x2–p)(x1–x2)=y22–y12=–2p(x1–x2).
显然x1≠x2(否则AB⊥x轴，l与x轴重合，与题设矛盾）得:
x1+x2–p=–2p即x1+x2=–p<0,这与x1+x2>0矛盾，
故直线l不能垂直平分线段AB.
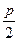，0）∈l. ∴|FA|=|FB|,设A（x1,y1）,B(x2,y2),显然x1>0,x2>0,y1≠y2,于是有（x1–
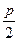）2+y12=(x2–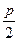)2+y22,整理得:（x1+x2–p)(x1–x2)=y22–y12=–2p(x1–x2).
显然x1≠x2(否则AB⊥x轴，l与x轴重合，与题设矛盾）得:
x1+x2–p=–2p即x1+x2=–p<0,这与x1+x2>0矛盾，
故直线l不能垂直平分线段AB.
练习册系列答案
作业辅导系列答案
相关题目
＋
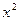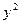－9x=0，与顶点在原点，焦点在x轴上的抛物线交于A、B两点，
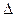OAB的垂心恰为抛物线的焦点，求抛物线的方程。
：
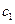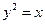和抛物线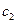
：
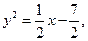是否存在直线
，使直线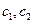
从下到上顺次交于点
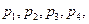且这些点的纵坐标
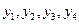组成等差数列？若存在，求出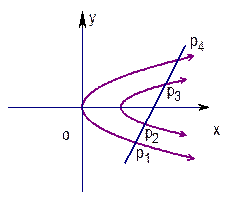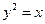直线
与直线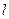
交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.
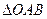面积的最小值.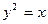
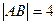
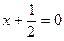
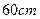，灯深是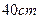
，则光源到反光镜顶点的距离是（ ）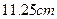
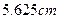
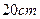
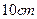
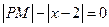，则动点P（x,y）的轨迹方程是 （ ）