题目内容
设函数 , 其中
, 其中 ,
, 是
是 的导函数.
的导函数.
(Ⅰ)若 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)若 ,函数
,函数 的两个极值点为
的两个极值点为 满足
满足 . 设
. 设 , 试求实数
, 试求实数 的取值范围.
的取值范围.
 , 其中
, 其中 ,
, 是
是 的导函数.
的导函数.(Ⅰ)若
 ,求函数
,求函数 的解析式;
的解析式;(Ⅱ)若
 ,函数
,函数 的两个极值点为
的两个极值点为 满足
满足 . 设
. 设 , 试求实数
, 试求实数 的取值范围.
的取值范围.(1) 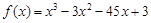 (2)
(2) 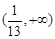
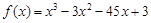 (2)
(2) 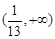
试题分析:(Ⅰ)据题意,
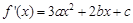 1分
1分由
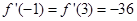
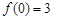 知,
知,据题意得
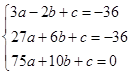 2分
2分解得
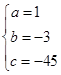 4分
4分故
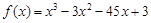 为所求. 5分
为所求. 5分(Ⅱ)据题意,
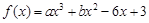 ,则
,则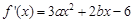
又
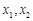 是方程
是方程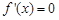 的两根,且
的两根,且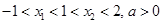
则
 即
即 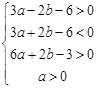 7分
7分则点
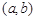 的可行区域如图 10分
的可行区域如图 10分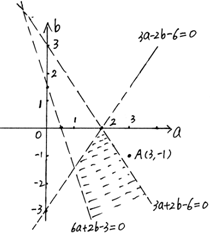
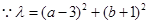
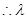 的几何意义为点P
的几何意义为点P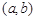 与点
与点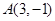 的距离的平方. 11分
的距离的平方. 11分观察图形知点,A到直线
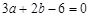 的距离的平方
的距离的平方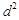 为
为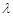 的最小值
的最小值 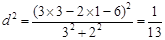
故
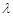 的取值范围是
的取值范围是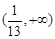 13分.
13分.点评:解决的关键是利用导数的运算以及函数与方程根的问题来得到不等式组来求解ab的区域,进而结合几何意义来得到范围。属于基础题。

练习册系列答案
相关题目
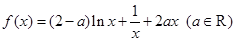 .
.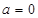 时,求
时,求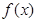 的极值;
的极值;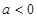 时,求
时,求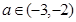 及
及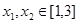 ,恒有
,恒有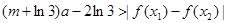 成立,求
成立,求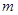 的取值范围
的取值范围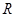 上的函数
上的函数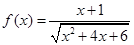 ,则
,则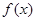 ( )
( )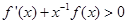 ,则函数
,则函数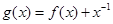 的零点的个数为( )
的零点的个数为( )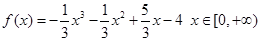 .
. 的极值;
的极值; 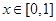 时,求
时,求 ,函数
,函数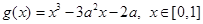 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数 的取值范围是( )
的取值范围是( )



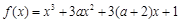 有极大值和极小值,则
有极大值和极小值,则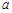 的取值范围是__ .
的取值范围是__ .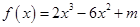 (
(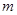 为常数)在
为常数)在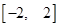 上有最大值3,那么此函数在
上有最大值3,那么此函数在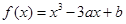 在点
在点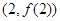 处与直线
处与直线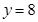 相切,则
相切,则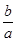 为 .
为 .