题目内容
在等差数列{an}中，若a4+a6+a8+a10+a12=40，则数列{an}前15项的和为________．
120
分析：有已知an为等差数列，设首项为a1和公差为d，则已知等式就为a1与d的关系等式，所求式子也可用a1和d来表示．
解答：∵an为等差数列且a4+a6+a8+a10+a12=5a1+35d=40
∴a1+7d=8
∴s15=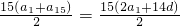
=15（a1+7d）=15×8=120
故答案为：120．
点评：此题主要考查了等差数列的通项公式，关键要熟悉公式并熟练运用公式．
分析：有已知an为等差数列，设首项为a1和公差为d，则已知等式就为a1与d的关系等式，所求式子也可用a1和d来表示．
解答：∵an为等差数列且a4+a6+a8+a10+a12=5a1+35d=40
∴a1+7d=8
∴s15=
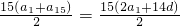=15（a1+7d）=15×8=120故答案为：120．
点评：此题主要考查了等差数列的通项公式，关键要熟悉公式并熟练运用公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目