题目内容
10.非零向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为不共线向量 $\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若$\overrightarrow{a}$与$\overrightarrow{b}$共线,则实数k的值是-2.分析 利用向量共线的充要条件列出方程,利用平面向量的基本定理求出k.
解答 解:$\overrightarrow{a}$与$\overrightarrow{b}$共线则存在λ使 $\overrightarrow{a}$=λ$\overrightarrow{b}$,即2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$=λ(k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$),
∴$\left\{\begin{array}{l}2=λk\\-1=λ\end{array}\right.$,
解得k=-2.
故答案为:-2.
点评 本题考查向量共线的充要条件、平面向量的基本定理,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设x3+ax+b=0,其中a,b均为实数,下列条件中,能使得该三次方程仅有一个实根的个数是( )
①a=-3,b=-3
②a=-3,b=2
③a=-3,b>2
④a=0,b=2
⑤a=1,b=2.
①a=-3,b=-3
②a=-3,b=2
③a=-3,b>2
④a=0,b=2
⑤a=1,b=2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.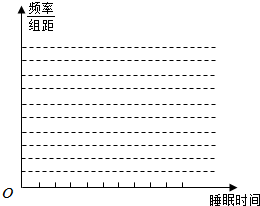 从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
(I)求n的值;
(Ⅱ)若a=10,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替.若上述数据的平均值为7.84,求a,b的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率.
 从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:| 组号 | 分组 | 频数 | 频率 |
| 1 | [5,6) | 2 | 0.04 |
| 2 | [6,7) | 0.20 | |
| 3 | [7,8) | a | |
| 4 | [8,9) | b | |
| 5[来源:Zxxk.Com] | [9,10) | 0.16 |
(Ⅱ)若a=10,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替.若上述数据的平均值为7.84,求a,b的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率.
19.已知△ABC中,a=1,b=$\sqrt{3}$,A=$\frac{π}{6}$,则B=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2}{3}$π | D. | $\frac{5}{6}$π或$\frac{π}{6}$ |
19.在△ABC中,b=1,c=$\sqrt{3}$,B=30°,则C的大小为( )
| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
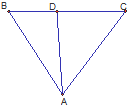 如图,已知A,B,C三点不共线.
如图,已知A,B,C三点不共线.
 B.
B.
 D.
D.