题目内容
7.设$\overrightarrow{a}$=(-1,1 ),$\overrightarrow{b}$=( 4,3 ),$\overrightarrow{c}$=( 5,-2 ),(1)求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值;
(2)求λ1和λ2,使$\overrightarrow{c}$=λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$.
分析 (1)利用平面向量的数量积公式求夹角;
(2)利用坐标表示$\overrightarrow{c}$=λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$,利用线段相等得到关于两个参数的方程组解之.
解答 解:(1)∵$\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(4,3)
$\overrightarrow{a}•\overrightarrow{b}$=-1×4+1×3=-1,|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=5,…(4分)
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-1}{5\sqrt{2}}$=-$\frac{\sqrt{2}}{10}$.…(6分)
(2)∵$\overrightarrow{c}$=λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$.
∴(5,-2)=λ1(-1,1)+λ2(4,3)=(-λ1+4λ2,λ1+3λ2) …(8分)
∴$\left\{\begin{array}{l}{-{λ}_{1}+4{λ}_{2}=5}\\{{λ}_{1}+3{λ}_{2}=-2}\end{array}\right.$….…(10分)
解得:$\left\{\begin{array}{l}{{λ}_{1}=-\frac{23}{7}}\\{{λ}_{2}=\frac{3}{7}}\end{array}\right.$…(12分)
点评 本题考查了利用平面向量的数量积的坐标表示求向量的夹角以及利用向量相等其参数;属于经常考查题型.

| A. | $\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2}{3}$π | D. | $\frac{5}{6}$π或$\frac{π}{6}$ |
| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
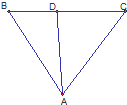 如图,已知A,B,C三点不共线.
如图,已知A,B,C三点不共线.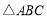 的一个内角为
的一个内角为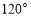 ,并且三边长构成公差为4的等差数列,则
,并且三边长构成公差为4的等差数列,则