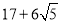题目内容
10.已知△ABC中,a=2$\sqrt{2}$,b=2$\sqrt{3}$,B=60°,那么角sinA等于( )| A. | -$\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 利用正弦定理即可得解.
解答 解:由正弦定理可得:sinA=$\frac{asinB}{b}=\frac{2\sqrt{2}×sin60°}{2\sqrt{3}}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题主要考查了正弦定理的应用,属于基础题.

练习册系列答案
相关题目
2. 从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
(I)求n的值;
(Ⅱ)若a=10,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替.若上述数据的平均值为7.84,求a,b的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率.
 从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:| 组号 | 分组 | 频数 | 频率 |
| 1 | [5,6) | 2 | 0.04 |
| 2 | [6,7) | 0.20 | |
| 3 | [7,8) | a | |
| 4 | [8,9) | b | |
| 5[来源:Zxxk.Com] | [9,10) | 0.16 |
(Ⅱ)若a=10,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替.若上述数据的平均值为7.84,求a,b的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率.
19.在△ABC中,b=1,c=$\sqrt{3}$,B=30°,则C的大小为( )
| A. | 30° | B. | 30°或150° | C. | 60°或120° | D. | 60° |
6.设函数f(x)=-x2+2x+3,x∈[-5,5].若从区间内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
9.函数f(x)=x2+ax+2在区间[1,5]上至少有一个零点,则实数a的取值范围为( )
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
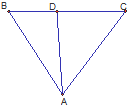 如图,已知A,B,C三点不共线.
如图,已知A,B,C三点不共线.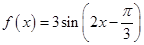 的图象为
的图象为 ,下列结论中正确的是( )
,下列结论中正确的是( ) 对称
对称 对称
对称 在区间
在区间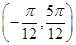 上递增
上递增 的图象向右平移
的图象向右平移 个单位长度可得
个单位长度可得
 B.
B.
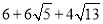 D.
D.