题目内容
5.若a是复数z1=$\frac{1+i}{2-i}$的实部,b是复数z2=(1-i)3的虚部,则ab等于$-\frac{2}{5}$.分析 根据复数代数形式的加减乘除运算法则分别化简z1、z2,整理出实部和虚部求出a、b的值,即可求出ab.
解答 解:由题意知,z1=$\frac{1+i}{2-i}$=$\frac{(1+i)(2+i)}{(2-i)(2+i)}$=$\frac{1+3i}{5}$=$\frac{1}{5}+\frac{3}{5}i$,
∴a=$\frac{1}{5}$,
∵z2=(1-i)3=-2i(1-i)=-2-2i,∴b=-2,
∴ab=$-\frac{2}{5}$,
故答案为:$-\frac{2}{5}$.
点评 本题考查复数代数形式的混合运算,掌握运算法则是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.关于x的方程x2-2x+5=0的一个根是1-2i,则另一根的虚部为( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
16.运行如图所示的程序框图,则输出k的值是( )
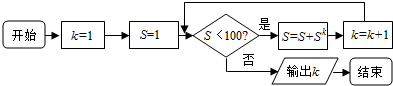

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.有4部车床需加工3个不同的零件,不同的安排方法有多少种?( )
| A. | 34 | B. | 43 | C. | 13 | D. | 14 |