题目内容
(本小题满分14分)
如图:某污水处理厂要在一个矩形污水处理池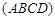 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道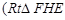 ,
,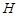 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口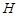 是
是 的中点,
的中点,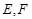 分别落在线段
分别落在线段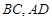 上。已知
上。已知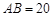 米,
米,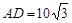 米,记
米,记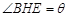 。
。

(Ⅰ)试将污水净化管道的长度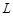 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)若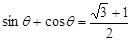 ,求此时管道的长度
,求此时管道的长度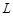 ;
;
(Ⅲ)问:当 取何值时,铺设管道的成本最低?并求出此时管道的长度。
取何值时,铺设管道的成本最低?并求出此时管道的长度。
【答案】
(Ⅰ)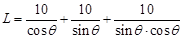 ,
,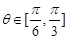 ;
;
(Ⅱ)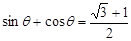 时,
时,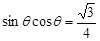 ,
,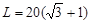 ;
;
(Ⅲ)当 时,所铺设管道的成本最低,此时管道的长度为
时,所铺设管道的成本最低,此时管道的长度为 米。
米。
【解析】本试题主要是考查了函数在实际函数中的运用。
(1)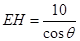 ,
, ,
,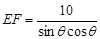
由于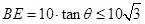 ,
,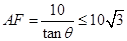 ,
,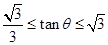 ,
,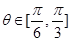 ,所以
,所以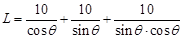 ,
,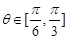 。
。
(2)因为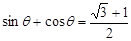 时,
时,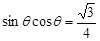 ,
,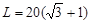
(3)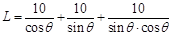 =
=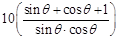 ,设
,设 ,
,
则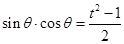 ,由于
,由于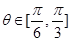 ,
,
构造二次函数,求解最值。
解:(Ⅰ)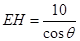 ,
, ,
,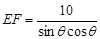
由于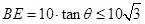 ,
,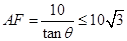 ,
,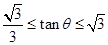 ,
,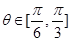 。3分
。3分
所以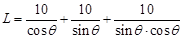 ,
,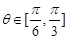 ……………………………5分
……………………………5分
(Ⅱ)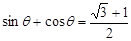 时,
时,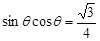 ,
,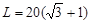 ;……………10分
;……………10分
(Ⅲ)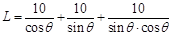 =
=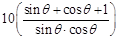 ,设
,设 ,
,
则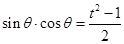 ,由于
,由于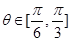 ,
,
所以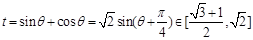 ,
,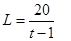 在
在 内单调递减,
内单调递减,
于是当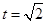 时
时 .
. 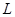 的最小值
的最小值 米……………………13分
米……………………13分
答:当 时,所铺设管道的成本最低,此时管道的长度为
时,所铺设管道的成本最低,此时管道的长度为 米………14分
米………14分

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)