Question

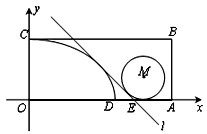在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y轴上（如图），且OC=1，OA=a+1（a＞1），点D在边OA上，满足OD=a．分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD．直线l：y=-x+b与椭圆弧相切，与OA交于点E．
（1）求证：b²-a²=1；
（2）设直线l将矩形OABC分成面积相等的两部分，求直线l的方程；
（3）在（2）的条件下，设圆M在矩形及其内部，且与l和线段EA都相切，求面积最大的圆M的方程．

Answer 1

分析：（1）设椭圆的方程为

x2

a2

+y2=1．由

x2 a2 +y2=1 y=-x+b

得（1+a²）x²-2a²bx+a²（b²-1）=0．由于直线l与椭圆相切，知△=（-2a²b）²-4a²（1+a²） （b²-1）=0，由此能够证明b²-a²=1．
（2）由题意知A（a+1，0），B（a+1，1），C（0，1），于是OB的中点为(

a+1

2

，  

1

2

)．因为l将矩形OABC分成面积相等的两部分，所以l过点(

a+1

2

，  

1

2

)，由此能求出直线l的方程．
（3）由E(

5

3

，  0)，  A(

7

3

，  0)．因为圆M与线段EA相切，所以可设其方程为（x-x₀）²+（y-r）²=r²（r＞0）．再由圆M在矩形及其内部和圆M与 l相切，且圆M在l上方，能够求出面积最大的圆M的方程．

解答：证明：（1）题设椭圆的方程为

x2

a2

+y2=1．…（1分）
由

x2 a2 +y2=1 y=-x+b

消去y得（1+a²）x²-2a²bx+a²（b²-1）=0．…（2分）
由于直线l与椭圆相切，故△=（-2a²b）²-4a²（1+a²） （b²-1）=0，
化简得b²-a²=1．①…（4分）
解：（2）由题意知A（a+1，0），B（a+1，1），C（0，1），
于是OB的中点为(

a+1

2

，  

1

2

)．…（5分）
因为l将矩形OABC分成面积相等的两部分，所以l过点(

a+1

2

，  

1

2

)，
即f（x），亦即2b-a=2．②…（6分）
由①②解得a=

4

3

，  b=

5

3

，故直线l的方程为y=-x+

5

3

．…（8分）
解：（3）由（2）知E(

5

3

，  0)，  A(

7

3

，  0)．
因为圆M与线段EA相切，所以可设其方程为（x-x₀）²+（y-r）²=r²（r＞0）．…（9分）
因为圆M在矩形及其内部，所以

0＜r≤ 1 2 x0＞ 5 3   x0+r≤ 7 3 ．

④…（10分）
圆M与 l相切，且圆M在l上方，所以

3(x0+r)-5

3 2

=r，即3(x0+r)=5+3

2

r．
…（12分）
代入④得

0＜r≤ 1 2 5+3( 2 -1)r 3 ＞ 5 3        5+3 2 r 3 ≤ 7 3 ，

即0＜r≤

2

3

．…（13分）
所以圆M面积最大时，r=

2

3

，这时，x0=

7- 2

3

．
故圆M面积最大时的方程为(x-

7- 2

3

)2+(y-

2

3

)2=

2

9

．…（15分）

点评：本题主要考查椭圆标准方程，简单几何性质，直线与椭圆的位置关系，圆的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．本题综合性强，是高考的重点，易错点是知识体系不牢固．