题目内容
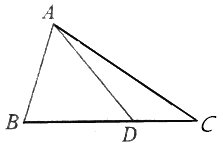
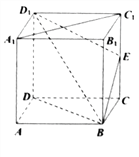
【题目】如图，直四棱柱
的所有棱长均为2， 
为
中点.
（Ⅰ）求证： 
平面
；
（Ⅱ）求证：平面
平面
.
【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析.
【解析】试题分析：
(Ⅰ) 连结
交
于
，取
中点
，连结
.由几何关系可证得四边形
为平行四边形，则以
，故
，利用线面平行的判定定理可得
平面
.
(Ⅱ) 
是菱形，则
，结合
平面
，可得
，利用线面垂直的判定定理可得
平面
，而
，故
平面
，结合面面垂直的判定定理可得平面
平面
.
试题解析：
(Ⅰ)连结
交
于
，取
中点
，连结
.
因为
，所以
是平行四边形，故
.
又
是
的中位线，故
，所以
，
所以四边形
为平行四边形.
所以
，所以
，
又
平面
， 
平面
，
所以
平面
.
(Ⅱ)因为
是菱形，所以
，
又
平面
， 
平面
，所以
，
又
，所以
平面
，
又
，所以
平面
，
又
平面
，所以平面
平面
.
【题目】2013年1月，北京经历了59年来雾霾天气最多的一个月．据气象局统计，北京市2013年1月1日至1月30日这30天里有26天出现雾霾天气，《环境空气质量指数(AQI)技术规定(试行)》如表1：
表1 空气质量指数AQI分组表
AQI指数M | 0～50 | 51～100 | 101～150 | 151～200 | 201～300 | >300 |
级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
表2是某气象观测点记录的连续4天里AQI指数M与当天的空气水平可见度y(km)的情况，表3是某气象观测点记录的北京市2013年1月1日至1月30日的AQI指数频数分布表．
表2 AQI指数M与当天的空气水平可见度y(km)的情况
AQI指数M | 900 | 700 | 300 | 100 |
空气水平可见度y(km) | 0.5 | 3.5 | 6.5 | 9.5 |
表3 北京市2013年1月1日至1月30日AQI指数频数分布表
AQI指数M | [0，200) | [200，400) | [400，600) | [600，800) | [800，1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x＝
，根据表2的数据，求出y关于x的线性回归方程．
(2)小王在北京开了一家洗车店，经小王统计：当AQI指数低于200时，洗车店平均每天亏损约2000元；当AQI指数在200至400时，洗车店平均每天收入约4000元；当AQI指数不低于400时，洗车店平均每天收入约7000元．
①估计小王的洗车店在2013年1月份平均每天的收入；
②从AQI指数在[0，200)和[800，1000]内的这6天中抽取2天，求这2天的收入之和不低于5000元的概率．
