题目内容
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的一条准线方程为x=
(a>b>0)的一条准线方程为x=![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
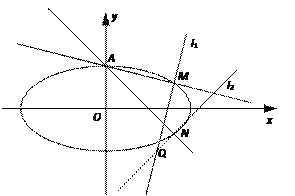
(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.
① 设直线AM,AN的斜率分别是k1, k2,求k1k2的值;
② 过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
【答案】(1) ![]() +y2=1.(2) ①
+y2=1.(2) ①![]() ② 点Q在一条定直线y=-1上
② 点Q在一条定直线y=-1上
【解析】试题分析:(1)根据题中条件得: 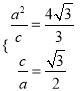 ,即可得解;
,即可得解;
(2)①根据椭圆的性质,M,N两点关于x轴对称,故可设M(x0,y0),N(x0,-y0)( x0≠0,y0≠0),由k1k2=![]() ,及点在椭圆上即可得解;
,及点在椭圆上即可得解;
②设Q(x1,y1),用坐标表示斜率,通过垂直得斜率之积为-1,可得(y0-1)(y1-y0)=-x0 (x1-x0),(-y0-1)(y1+y0)=-x0 (x1-x0),化得(y1+1) y0=0,所以y1=-1,得证.
试题解析:
(1)设椭圆C:![]() +
+![]() =1的半焦距为c.
=1的半焦距为c.
由题意,得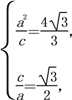 解得
解得 从而b=1.
从而b=1.
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)①根据椭圆的性质,M,N两点关于x轴对称,
故可设M(x0,y0),N(x0,-y0)( x0≠0,y0≠0),
从而 k1k2=![]() ·
·![]() =
=![]() .
.
因为点M在椭圆C上,所以![]() +y02=1,所以1-y02=
+y02=1,所以1-y02=![]() ,
,
所以k1k2=![]() =
=![]() .
.
②设Q(x1,y1),依题意A(0,1).
因为l1⊥AM,所以![]() ·
·![]() =-1,即(y0-1)(y1-y0)=-x0 (x1-x0);
=-1,即(y0-1)(y1-y0)=-x0 (x1-x0);
因为l2⊥AN,所以![]() ·
·![]() =-1,即(-y0-1)(y1+y0)=-x0 (x1-x0),
=-1,即(-y0-1)(y1+y0)=-x0 (x1-x0),
故 (y0-1)(y1-y0)-(-y0-1)(y1+y0)=0,
化得(y1+1) y0=0.
从而必有y1+1=0,即y1=-1.
即点Q在一条定直线y=-1上.