题目内容
已知:f(x)=-sin2x+sinx+a
(Ⅰ)当f(x)=0有实数解时,求实数a的取值范围;
(Ⅱ)若x∈R恒有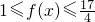 成立,求实数a的取值范围.
成立,求实数a的取值范围.
解:(1)因为f(x)=0,即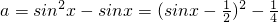 ,a的最大值等于
,a的最大值等于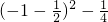 =2,
=2,
a的最小值等于- ,所以,
,所以,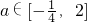 .
.
(2)f(x)=-sin2x+sinx+a= ,∴
,∴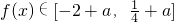 ,
,
又∵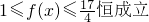 ,∴
,∴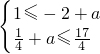 ,∴3≤a≤4.
,∴3≤a≤4.
所以,实数a的取值范围是[3,4].
分析:(1) 利用二次函数的性质及正弦函数的值域求出a的最大值和a的最小值,即得实数a的取值范围.
(2)f(x)配方后结合正弦函数的值域,求出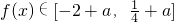 ,再根据
,再根据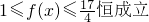 ,
,
得到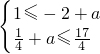 ,从而得到实数a的取值范围.
,从而得到实数a的取值范围.
点评:本题考查三角函数的最值,函数的恒成立问题,以及正弦函数的有界性,得到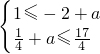 是解题的难点.
是解题的难点.
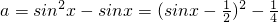 ,a的最大值等于
,a的最大值等于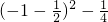 =2,
=2,a的最小值等于-
 ,所以,
,所以,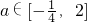 .
.(2)f(x)=-sin2x+sinx+a=
 ,∴
,∴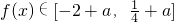 ,
,又∵
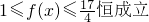 ,∴
,∴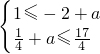 ,∴3≤a≤4.
,∴3≤a≤4.所以,实数a的取值范围是[3,4].
分析:(1) 利用二次函数的性质及正弦函数的值域求出a的最大值和a的最小值,即得实数a的取值范围.
(2)f(x)配方后结合正弦函数的值域,求出
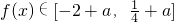 ,再根据
,再根据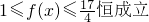 ,
,得到
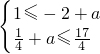 ,从而得到实数a的取值范围.
,从而得到实数a的取值范围.点评:本题考查三角函数的最值,函数的恒成立问题,以及正弦函数的有界性,得到
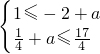 是解题的难点.
是解题的难点. 
练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目