题目内容
(2013•惠州一模)已知函数f(x)=ax2+bx+1在x=3处的切线方程为y=5x-8.
(1)求函数f(x)的解析式;
(2)若关于x的方程f(x)=kex恰有两个不同的实根,求实数k的值;
(3)数列{an}满足2a1=f(2),an+1=f(an),n∈N*,求S=
+
+
+…+
的整数部分.
(1)求函数f(x)的解析式;
(2)若关于x的方程f(x)=kex恰有两个不同的实根,求实数k的值;
(3)数列{an}满足2a1=f(2),an+1=f(an),n∈N*,求S=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
分析:(1)把x=3代入切线方程,求出切点,把切点坐标代入二次函数得关于a,b方程,再由f′(3)=5得另一方程,联立求解a,b的值,则函数解析式可求;
(2)把(1)中求出函数f(x)的解析式代入方程f(x)=k ex,然后转化为k=e-x(x2-x+1),然后利用导数求函数g(x)=e-x(x2-x+1)的极值,根据函数g(x)的极值情况,通过画简图得到使方程k=e-x(x2-x+1),即方程f(x)=k ex恰有两个不同的实根时的实数k的值;
(3)由2a1=f(2)求出a1,结合an+1=f(an),n∈N*求出a2,并判断出数列{an}为递增数列,进一步由an+1=f(an),n∈N*得到
=
-
,分别取n=1,2,…,代入S=
+
+
+…+
后化简,则S=
+
+
+…+
的整数部分可求.
(2)把(1)中求出函数f(x)的解析式代入方程f(x)=k ex,然后转化为k=e-x(x2-x+1),然后利用导数求函数g(x)=e-x(x2-x+1)的极值,根据函数g(x)的极值情况,通过画简图得到使方程k=e-x(x2-x+1),即方程f(x)=k ex恰有两个不同的实根时的实数k的值;
(3)由2a1=f(2)求出a1,结合an+1=f(an),n∈N*求出a2,并判断出数列{an}为递增数列,进一步由an+1=f(an),n∈N*得到
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
解答:解:(1)由f(x)=a x2+bx+1,所以f′(x)=2ax+b,
因为函数f(x)=a x2+bx+1在x=3处的切线方程为y=5x-8,所以切点为(3,7).
则
,解得:a=1,b=-1.
所以f(x)=x2-x+1;
(2)由(1)知f(x)=x2-x+1,
关于x的方程f(x)=kex恰有两个不同的实根,
即x2-x+1=k•ex有两个不同的实根,也就是k=e-x(x2-x+1)有两个不同的实根.
令g(x)=e-x(x2-x+1),
则g′(x)=(2x-1)e-x-(x2-x+1)e-x
=-(x2-3x+2)e-x=-(x-1)(x-2)e-x
由g′(x)=0,得x1=1,x2=2.
所以当x∈(-∞,1)时,g′(x)<0,g(x)在(-∞,1)上为减函数;
当x∈(1,2)时,g′(x)>0,g(x)在(1,2)上为增函数;
当x∈(2,+∞)时,g′(x)<0,g(x)在(2,+∞)上为减函数;
所以,当x=1时,g(x)取得极小值g(1)=
,当x=2时函数取得极大值g(2)=
.
函数y=k与y=g(x)的图象的大致形状如下,

由图象可知,当k=
和k=
时,关于x的方程f(x)=kex恰有两个不同的实根;
(3)由2a1=f(2)=22-2+1=3,所以a1=
>1,a2=a12-a1+1=(
)2-
+1=
.
又an+1-an=an2-2an+1=(an-1)2>0,
所以an+1>an>1.
又an+1=f(an)=an2-an+1,所以an+1-1=an(an-1),
则
=
-
,即
=
-
.
所以S=
+
+
+…+
=(
-
)+(
-
)+…+(
-
)
=
-
=
-
=2-
<2.
又S=
+
=
+
=
+
=
>1.
故S=
+
+
+…+
的整数部分等于1.
因为函数f(x)=a x2+bx+1在x=3处的切线方程为y=5x-8,所以切点为(3,7).
则
|
所以f(x)=x2-x+1;
(2)由(1)知f(x)=x2-x+1,
关于x的方程f(x)=kex恰有两个不同的实根,
即x2-x+1=k•ex有两个不同的实根,也就是k=e-x(x2-x+1)有两个不同的实根.
令g(x)=e-x(x2-x+1),
则g′(x)=(2x-1)e-x-(x2-x+1)e-x
=-(x2-3x+2)e-x=-(x-1)(x-2)e-x
由g′(x)=0,得x1=1,x2=2.
所以当x∈(-∞,1)时,g′(x)<0,g(x)在(-∞,1)上为减函数;
当x∈(1,2)时,g′(x)>0,g(x)在(1,2)上为增函数;
当x∈(2,+∞)时,g′(x)<0,g(x)在(2,+∞)上为减函数;
所以,当x=1时,g(x)取得极小值g(1)=
| 1 |
| e |
| 3 |
| e2 |
函数y=k与y=g(x)的图象的大致形状如下,

由图象可知,当k=
| 1 |
| e |
| 3 |
| e2 |
(3)由2a1=f(2)=22-2+1=3,所以a1=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 4 |
又an+1-an=an2-2an+1=(an-1)2>0,
所以an+1>an>1.
又an+1=f(an)=an2-an+1,所以an+1-1=an(an-1),
则
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
所以S=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
=(
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| a2012-1 |
| 1 |
| a2013-1 |
=
| 1 |
| a1-1 |
| 1 |
| a2013-1 |
| 1 | ||
|
| 1 |
| a2013-1 |
| 1 |
| a2013-1 |
又S=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 4 |
| 7 |
| 25 |
| 21 |
故S=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
点评:本题考查了利用导数研究曲线上某点的切线方程,考查了函数解析式的求解及常用方法,考查了函数的零点与方程根的关系,考查了数列的和,解答此题的关键在于构造函数,然后利用导数分析函数的极值借助于函数图象的大致形状分析函数零点的情况,是难度较大的题目.

练习册系列答案
相关题目
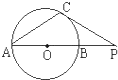 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题)