题目内容
已知函数f(x)在R上可导,且f(x)=x2+2xf ′(2),则f (-1)与f (1)的大小关系为
| A.f(-1)= f(1) | B.f(-1)>f(1) |
| C.f(-1)< f(1) | D.不确定 |
B
分析:由f(x)的解析式,利用求导法则求出f(x)的导函数,把x=1代入导函数中求出f′(1)的值,从而确定出f(x)的解析式,然后分别把x等于1和-1代入即可求出f(1)和f(-1)的值,即可比较出大小.
解答:解:由f(x)=x2+2xf′(1),求导得f′(x)=2x+2f′(1),
把x=1代入得:f′(1)=2+2f′(1),
解得:f′(1)=-2,∴f(x)=x2-4x,
∴f(-1)=(-1)2-4×(-1)=5,f(1)=12-4×1=-3,
则f(-1)>f(1).
故选B
解答:解:由f(x)=x2+2xf′(1),求导得f′(x)=2x+2f′(1),
把x=1代入得:f′(1)=2+2f′(1),
解得:f′(1)=-2,∴f(x)=x2-4x,
∴f(-1)=(-1)2-4×(-1)=5,f(1)=12-4×1=-3,
则f(-1)>f(1).
故选B

练习册系列答案
相关题目
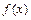 满足:①对任意的
满足:①对任意的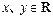 ,都有
,都有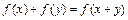 ;②当
;②当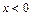 时,有
时,有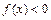 .
.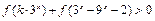 在
在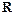 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.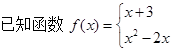

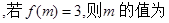 ( )
( )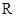 上的函数
上的函数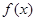 满足
满足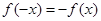 ,当
,当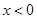 时,
时,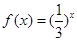 ,则
,则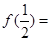
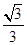
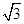
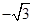
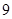
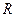 的函数
的函数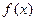 是偶函数,当
是偶函数,当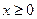 时,
时,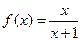 .
.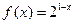 在区间
在区间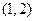 上有解
上有解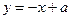 与曲线
与曲线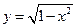 有两个交点,则
有两个交点,则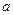 的取值范围是
的取值范围是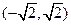
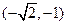
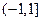
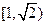
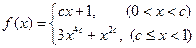 ,若
,若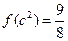 ,则不等式
,则不等式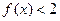 的解集为
的解集为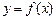 是奇函数,当
是奇函数,当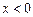 时,
时,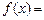
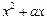
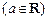 ,且
,且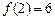 ,则
,则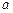 = .
= . ,则
,则 = .
= .